Defining a User-Coded Energy Source in a Parcel
In simple cases, internal heating of particles can be modeled using field functions, but more complex cases can be modeled with user coding. This example compares the two methods for a transient simulation injecting aluminum particles into a square box.
A constant energy source of 1.0E8 W/m3 heats the particles during the 0.05 seconds of simulation time, raising their temperature from 300 to 301.12 degrees. Since the heat source is constant, the temperature increases linearly with residence time.
Parts of the parcel profile can become invalid due to other physical processes occurring during a substep of the Lagrangian solution procedure. The user code must check the parcelId for validity before operating on the profile. The profile must have the parcelId passed in as an argument in addition to the arguments necessary to calculate the heat source.
The subroutine uflib.f registers the parcelId and the temperature:
subroutine uflib()
use StarRealMod
implicit none
c Register user functions
external parcelQdot
call uffunc(parcelQdot,
& "ParcelProfile",
& "Parcel Heat Source")
call ufarg(parcelQdot,
& "Parcel",
& "ParcelId",
& StarInt)
return
endThe user code that applies the heat source to the parcels in the domain is:
subroutine parcelQdot(result,size,Id)
c parcel heat source example
use StarRealMod
integer, intent(in) :: size
real(StarReal), intent(out) :: result(size)
real(StarInt), intent(in) :: Id(*)
real(StarInt), parameter :: NULL_INDEX = -1
integer i
do i = 1, size
if (Id(i) .gt. NULL_INDEX) then
result(i) = 1e8
endif
end do
return
endWhen compared to the internal user-defined heat source, the field functions and the user code above have identical results:
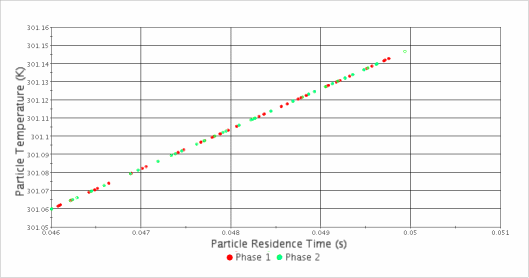
In the plot above, Phase 1 corresponds to the internally calculated parcel heat flux and Phase 2 corresponds to the user-coded parcel heat flux. Since the particle times are staggered slightly during the injection process for this case, the residence times differ slightly. In both cases, however the particle temperature is linearly proportional to residence time.