Field Histories Example: Pressure-Time Derivatives

Field histories provide, among other uses, the ability to compute time derivatives of solution quantities. However, you must correctly account for any motion in the field.

Examples of applications include:

  • Using a pressure derivative to investigate acoustics
  • Using momentum time derivatives to detect sources of fatigue through fluctuations in force/moment
  • Using turbulent kinetic energy time derivatives to identify power fluctuations

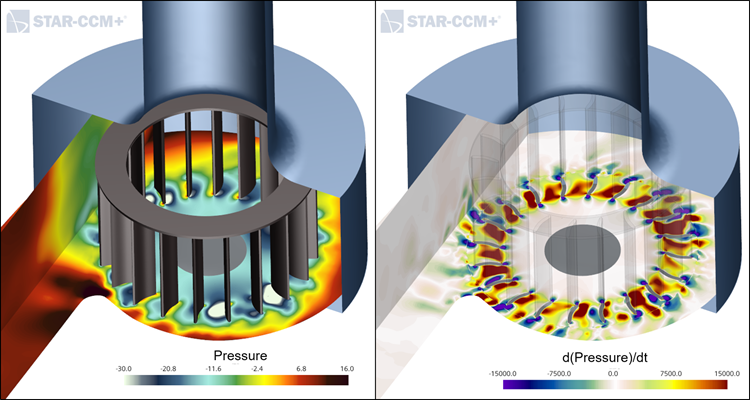
Pressure-Time Derivative in a Squirrel Cage Blower

In the illustration below for a squirrel cage blower, pressure contours are shown on the left and d p / d t (second order error, backward difference formulation) is shown on the right. This data was created using field functions that leverage field history stored results.



The field histories defined for this case are:
  • History of Position:
    • Sliding Sample Window Size: 2
    • Field Function: Position
    • Trigger: Time Step
    • Resulting field function names: History of Position Sample 0, History of Position Sample 1
  • History of Pressure:
    • Sliding Sample Window Size: 2 or more (depending on stencil width)
    • Field Function: Pressure
    • Trigger: Time Step
    • Resulting field function names: History of Pressure Sample 0, History of Pressure Sample 1, and so on

From basic transport equations, the substantial or material derivative for pressure is:

D p D t = ∂ p ∂ t + v ⋅ ∇ p

Hence to obtain the pressure derivative in a simulation with mesh motion, you must evaluate:

∂ p ∂ t = D p D t − v ⋅ ∇ p

The mesh velocity in each cell can be obtained using a field history that samples Position, and for which the resulting field functions are HistoryofPositionSample0 (current time-step) and HistoryofPositionSample1 (previous time-step). These are combined in a field function MeshVelocity as:

MeshVelocity = ($${HistoryofPositionSample0}-$${HistoryofPositionSample1})/${dt}

where dt is another field function that contains the time-step. This function can be supplied as a scalar parameter.

The velocity-gradient term can be computed by a field function, Pconvective_current:

Pconvective_current = dot($${MeshVelocity},grad(${Pressure}))

Where Pressure is the built-in solution field function.

For computing the final pressure derivative, the simplest first order computation using field functions from the field history of pressure is:

(${HistoryofPressureSample0}-${HistoryofPressureSample1})/(1.0*${dt}) - ${Pconvective_current}

A more complex expression, with a wider stencil (and requiring a Sliding Sample Window Size of 3 for Pressure), is:

(3.0*${HistoryofPressureSample0}-4.0*${HistoryofPressureSample1}+${HistoryofPressureSample2})/(2.0*${dt}) - ${Pconvective_current}

Using time derivative expressions with higher order accuracy can help to reduce the noise, but at the cost of an increased size for the simulation file.

If your simulation has no motion, then Pconvective_current is not required.

Bibliography

[142]
James, M.L., Smith, G.M., and Wolford, J.C. 1977. "Applied Numerical Methods for Digital Computation with FORTRAN and CSMP", 2nd ed. Harper & Row.