Home
Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
Heat Transfer and Radiation
The tutorials in this set illustrate various Simcenter STAR-CCM+ features for heat transfer, radiation, and thermal comfort.
Natural Convection: Concentric Cylinders Introduction
This tutorial demonstrates how to solve a natural convection problem in Simcenter STAR-CCM+.
Comparing Results to Experimental Data
This part of the tutorial compares results and data using equivalent conductivity.

Share

Link: copied

Breadcrumb: copied

Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
- Using Tutorial Macros and Files
  Macros, input files, and final simulation files for a range of tutorials are provided as an optional download package on the Support Center website. These macros and final simulation files are provided as an aid to the written tutorials, so that you can check your final results against the downloaded files, or against a simulation that is built and run using the macros.
- Introduction
  Welcome to the Simcenter STAR-CCM+ introductory tutorial. In this tutorial, you explore the important concepts and workflow. Complete this tutorial before attempting any others.
- Foundation Tutorials
  The foundation tutorials showcase the major features of Simcenter STAR-CCM+ in a series of short tutorials.
- Geometry
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for creating and working with parts and 3D-CAD.
- Mesh
  The tutorials in this set illustrate various STAR-CCM+ features for building CFD meshes.
- Incompressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for incompressible fluid flows as well as porosity and solution recording
- Compressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for compressible fluid flows as well as harmonic balance.
- Heat Transfer and Radiation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for heat transfer, radiation, and thermal comfort.
  - Conjugate Heat Transfer: Heated Fin Introduction
    This tutorial incorporates both multi-region conjugate heat transfer and natural convection in a Simcenter STAR-CCM+ simulation.
  - Simulation Operations: Multi-Timescale Conjugate Heat Transfer
    Through simulation operations, Simcenter STAR-CCM+ provides an automated methodology by which you can include a multiple time-scale workflow in a single simulation.
  - Simulation Operations: Transient-transient Multi-Timescale Conjugate Heat Transfer
    An important analysis for automotive applications is to simulate the thermal behavior of components during cold-start conditions. As the timescales involved in fluctuating fluid behavior often varies significantly from the timescales in solid thermal behavior, it is not efficient to run an implicitly coupled conjugate heat transfer simulation. Simcenter STAR-CCM+ provides a coupling strategy that permits distinct transient timescales for the solid and fluid components.
  - Multi-Part Solid: Graphics Card Cooling
    This tutorial demonstrates how you can model multiple solid parts in a single continuum using the Multi-Part Solid physics model.
  - Natural Convection: Concentric Cylinders Introduction
    This tutorial demonstrates how to solve a natural convection problem in Simcenter STAR-CCM+.
    - Prerequisites
      The instructions in the Natural Convection tutorial assume that you are already familiar with certain techniques in Simcenter STAR-CCM+.
    - Importing the Mesh and Naming the Simulation
      To set up the Simcenter STAR-CCM+ simulation, launch a simulation and import the supplied volume mesh.
    - Setting Up the Physics Models
      Set up the physics using an implicit coupled flow solver due to its increased robustness over the segregated solver.
    - Setting Boundary Physics Conditions
      A fixed temperature difference across the annulus is achieved by setting the static temperatures of the inner and outer cylinder walls.
    - Preparing Scalar and Vector Scenes
      A scalar and a vector scene are created to display the temperature and velocity vectors in the region bounded by the concentric cylinders during the simulation.
    - Preparing Reports to Monitor Convergence
      To judge convergence for this natural convection problem, monitor the heat balance in your model, which sums to zero for a converged case.
    - Running the Simulation
      The simulation is now ready to run.
    - Visualizing the Results
      The scalar and vector scenes contain the solution results.
    - Comparing Results to Experimental Data
      This part of the tutorial compares results and data using equivalent conductivity.
    - Summary
      The Natural Convection tutorial used two concentric cylinders to introduce a variety of Simcenter STAR-CCM+ features.
    - References
      This tutorial repeats the experiments of Kuehn and Goldstein (1978).
  - Electronics Cooling Toolset: Natural Convection JEDEC
    Although many electronic devices benefit from cooling fans in removing excess heat, some devices rely on natural convection only. The Electronics Cooling Toolset includes a method for estimating cooling due to natural convection.
  - Electronics Cooling Toolset: Graphics Card Cooling
    When you are positioning fans that cool electronic components, the Electronics Cooling Toolset allows you to assess the impact that they have on removing heat. By comparing multiple designs, you can decide which arrangement gives you the best performance.
  - Dual Stream Heat Exchanger: Car Radiator
    Heat exchangers are devices that efficiently transfer heat from one medium to another. Some prominent examples of heat exchanger applications include car radiators, such as the one used in this tutorial, power plants and air-conditioning.
  - Surface-to-Surface Radiation: Thermal Insulator
    This tutorial incorporates gray thermal radiation in a Simcenter STAR-CCM+ simulation.
  - Multiband Surface-to-Surface Radiation: Solar Collector
    This tutorial uses the simulation created for the Surface-to-Surface Radiation: Thermal Insulator.
  - Photon Monte Carlo Radiation: Headlamp
    Thermal management simulations of headlamp applications allow you to identify temperature hotspots that can cause damage to the headlamp. Modifying the design—for example, including heat shields in the right places—leads to better and more durable designs.
  - Thermal Comfort: Car Cabin
    Comfort is one of the main factors that consumers consider when deciding how they travel. Therefore, passenger comfort is one of the key criteria that influence the design process of enclosed spaces such as a car or aircraft cabin.
  - Parts-Based Shells: Exhaust Pipe
    Simcenter STAR-CCM+ provides support for thin-walled structures that are best represented by a single-cell layer during simulation. These single-cell layers are known as shells. One of the main advantages of using shell elements is that it reduces the computational time and resources required for simulations.
- Multiphase Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating multiphase fluid flow problems
- Discrete Element Method
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating Discrete Element Method problems
- Motion
  The tutorials in this set illustrate various STAR-CCM+ features for simulating problems with moving geometries and meshes, dynamic fluid body interaction, and rigid body motion:
- Reacting Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating reacting flows such as combustion.
- Solid Stress
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for computing deformation, strain, and stresses in solid regions. They also show how such computations can be coupled to the fluid behavior in an analysis of fluid-structure interaction.
- Aeroacoustics
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for solving aeroacoustic simulations.
- Electromagnetism
  The following tutorials illustrate features for solving problems that involve electromagnetic fields.
- Electrochemistry
  The following tutorial demonstrates chemical reactions induced by an electrical current.
- Battery
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for setting up a battery model:
- Automation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ automation and macro features.
- Design Exploration
  The tutorials in this set illustrate various features for running design exploration studies in Design Manager.
- Coupling with CAE Codes
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for coupling with CAE codes:
- Analysis Methods
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for analysing and visualizing simulation data.
- Simcenter STAR-CCM+ In-cylinder
  The tutorials in this set illustrate features for simulating internal combustion engines in Simcenter STAR-CCM+ using the dedicated add-on Simcenter STAR-CCM+ In-cylinder.

Comparing Results to Experimental Data

This part of the tutorial compares results and data using equivalent conductivity.

Kuehn and Goldstein reported their experimental and numerical results in the form of an equivalent conductivity. This equivalent conductivity is defined as the ratio of the actual heat transfer measured (or predicted) across the annulus to the heat transfer that would be obtained by pure conduction alone. That is:

Figure 1. EQUATION_DISPLAY

k_{e q} = \frac{q_{a c t}}{q_{c o n d}}

(5248)

For concentric cylinders, $q_{c o n d}$ is defined as:

Figure 2. EQUATION_DISPLAY

q_{c o n d} = \frac{2 π k Δ T}{\ln (R_{o} / R_{i})}

(5249)

For the case being considered in this tutorial, Kuehn and Goldstein obtained an equivalent conductivity of 2.58.

To begin evaluating conductivity, calculate the conductive heat transfer based on Eqn. (5249) using values provided earlier in your setup. This comes out to $q_{c o n d} = 2.177 W / m$ .
To retrieve the value of $q_{a c t}$ for one half of the cylinders, double-click the Heat Transfer Inner or Heat Transfer Outer node under Reports.
The heat transfer appears in the Output window.

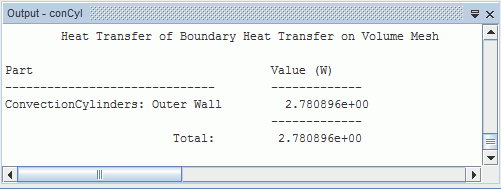
The total $q_{a c t}$ for the complete annulus is therefore 5.56 W.

Inserting this value into Eqn. (5248) above calculates an equivalent conductivity of:

$k_{e q} = \frac{5.56}{2.177} = 2.55$

(5250)

There is only about a 1% difference between this result and the value given by Kuehn and Goldstein, showing that the numerical model has predicted the heat transfer consistent to what has been reported by others.

Note Because you are working with a 2D representation of the cylinders, the prediction of heat transfer is per meter length, that is, W/m.