Home
Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
Electromagnetism
The following tutorials illustrate features for solving problems that involve electromagnetic fields.
Magnetic Vector Potential: Axial Flux Motor
This tutorial demonstrates how to use the Finite Element Magnetic Potential Vector model to solve for the magnetic flux produced by the magnets of an axial-flux motor.

Share

Link: copied

Breadcrumb: copied

Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
- Using Tutorial Macros and Files
  Macros, input files, and final simulation files for a range of tutorials are provided as an optional download package on the Support Center website. These macros and final simulation files are provided as an aid to the written tutorials, so that you can check your final results against the downloaded files, or against a simulation that is built and run using the macros.
- Introduction
  Welcome to the Simcenter STAR-CCM+ introductory tutorial. In this tutorial, you explore the important concepts and workflow. Complete this tutorial before attempting any others.
- Foundation Tutorials
  The foundation tutorials showcase the major features of Simcenter STAR-CCM+ in a series of short tutorials.
- Geometry
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for creating and working with parts and 3D-CAD.
- Mesh
  The tutorials in this set illustrate various STAR-CCM+ features for building CFD meshes.
- Incompressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for incompressible fluid flows as well as porosity and solution recording
- Compressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for compressible fluid flows as well as harmonic balance.
- Heat Transfer and Radiation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for heat transfer, radiation, and thermal comfort.
- Multiphase Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating multiphase fluid flow problems
- Discrete Element Method
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating Discrete Element Method problems
- Motion
  The tutorials in this set illustrate various STAR-CCM+ features for simulating problems with moving geometries and meshes, dynamic fluid body interaction, and rigid body motion:
- Reacting Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating reacting flows such as combustion.
- Solid Stress
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for computing deformation, strain, and stresses in solid regions. They also show how such computations can be coupled to the fluid behavior in an analysis of fluid-structure interaction.
- Aeroacoustics
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for solving aeroacoustic simulations.
- Electromagnetism
  The following tutorials illustrate features for solving problems that involve electromagnetic fields.
  - Ohmic Heating: Domestic Fuse
    This tutorial demonstrates some of the capabilities of the Ohmic Heating model available in Simcenter STAR-CCM+.
  - Magnetic Vector Potential: Axial Flux Motor
    This tutorial demonstrates how to use the Finite Element Magnetic Potential Vector model to solve for the magnetic flux produced by the magnets of an axial-flux motor.
    - Prerequisites
      To complete this tutorial, you require a double-precision version of Simcenter STAR-CCM+. Also, the instructions in this tutorial assume that you are already familiar with certain techniques in Simcenter STAR-CCM+.
    - Importing the Geometry
      In this tutorial, you are provided with a CAD model representing 1/8 of the geometry. From this CAD model, you create geometry parts for the magnet, the magnet plate, the stator plate, and the surrounding air.
    - Selecting the Physics Models
      In this simulation, you study the steady state distribution of the magnetic flux density throughout the motor components. This simulation requires two physics continua, one for the air region and one for the motor components.
    - Creating Periodic Contacts
      To simulate the behavior of the full geometry model, you create periodic contacts between the part surfaces of the reduced geometry.
    - Preparing the Regions and Generating the Mesh
      Assign the geometry parts to regions, creating the required boundaries and interfaces, and generate a mesh of tetrahedral elements. Tetrahedral elements are suitable for finite element solvers.
    - Defining Material Properties and Interface Conditions
      To define the magnetic behavior of the motor, you specify the magnetic permeability of its components and the residual magnetic flux density of the permanent magnet. As you model a single magnet (1/8 of the geometry), rather than a pair of magnets with opposite polarity (1/4 of the geometry), you use antiperiodic interface conditions that account for the different polarity at the two sides of the interface.
    - Preparing for Analysis
      Create a scalar scene to display the Z-component of the magnetic flux density on the magnet. Also, create a plot to display the flux density along a line contour directed along the radius of the magnet plate.
    - Running the Simulation
      Run the simulation to solve for the magnetic flux.
    - Visualizing the Results
      You can visualize the magnetic flux density available for torque production in the scalar scene and XY plot that you created in the previous sections.
    - Summary
      This tutorial demonstrated how to calculate a 3D magnetic flux field from magnets in a slotless permanent-magnet brushless motor.
  - Magnetohydrodynamics: Stirring Induced by Excitation Coils
    In this tutorial, you simulate the electromagnetic stirring of molten metal induced by excitation coils.
  - Airgap Remeshing: Electronic Speedometer
    Electric machine simulations require a conformal mesh at the interfaces between different components. Airgap remeshing is a meshing technique that allows you to generate and maintain conformal meshes between regions that are in relative motion.
  - Higher Order Magnetic Vector Potential: Axial Flux Motor
    Axial flux motors have, over recent years, become increasingly more popular for aerospace and automotive applications. One of the main advantages of axial flux motors is their high power density, which allows for high efficiency in compact designs.
  - Electric Circuits: Full-Wave Rectifier
    In power electronics, a full-wave rectifier provides rectification from an AC (Alternating Current) wave to a DC supply. Simcenter STAR-CCM+ provides simulation capabilities that allow you to investigate the effect of circuit component choices on the electromagnetic performance of such devices.
- Electrochemistry
  The following tutorial demonstrates chemical reactions induced by an electrical current.
- Battery
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for setting up a battery model:
- Automation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ automation and macro features.
- Design Exploration
  The tutorials in this set illustrate various features for running design exploration studies in Design Manager.
- Coupling with CAE Codes
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for coupling with CAE codes:
- Analysis Methods
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for analysing and visualizing simulation data.
- Simcenter STAR-CCM+ In-cylinder
  The tutorials in this set illustrate features for simulating internal combustion engines in Simcenter STAR-CCM+ using the dedicated add-on Simcenter STAR-CCM+ In-cylinder.

Magnetic Vector Potential: Axial Flux Motor

This tutorial demonstrates how to use the Finite Element Magnetic Potential Vector model to solve for the magnetic flux produced by the magnets of an axial-flux motor.

An axial-flux, or “pancake”, motor is a disc-type electric motor where magnets are arrayed on a rotor around a central shaft. This type of motor is typically used in applications that require a short axial length, for example in elevators where the lifting gear is located inside the elevator shaft.

The main flux in an axial-flux motor passes through an air gap between the rotor and stator in a direction parallel to the axis of rotation. The three-dimensional magnetic flux distribution the motor produces is difficult to calculate using analytical methods.

This simulation models 1/8 of a slotless permanent-magnet brushless motor, surrounded by air. In the full geometry, magnetic poles of opposite polarity (north and south) alternate around the central shaft. In the reduced geometry, you model a single magnetic pole and use antiperiodic interface conditions to account for the change in polarity.

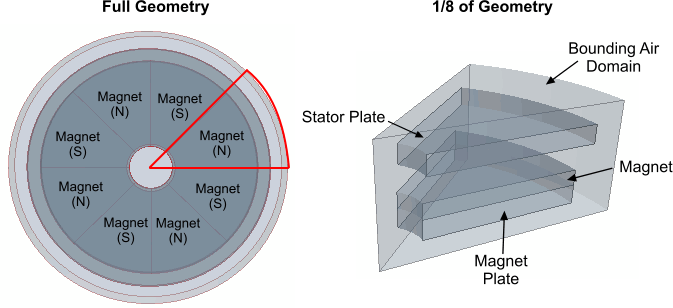
The windings, which would be located in the gap between the rotor and the stator, are not shown, as they are not used in the simulation.

Analysis Overview


Geometry	1/8 of the full geometry
Mesh	Linear tetrahedral elements Conformal interfaces
Materials and Physics	Materials: Bounding domain: Air Motor Components: Steel with constant magnetic permeability (linear magnetization assumption) Main Physics Models: Finite Element Magnetic Potential Vector to solve for magnetic flux density Permanent Magnet to model the effects of a permanent magnet
Boundary Conditions	Anti-Symmetry Perfect Electric Conductor (PEC) assumption for all boundaries.
Interfaces	internal interfaces between contacting regions periodic interfaces with antiperiodic magnetic vector potential, to replicate the behavior of the full geometry
Discretization and Solution Method	Finite Element (FE) method