Solution Data Interpolation

Many operations require interpolation of solution data between different sets of mesh points. For example, remeshing operations require interpolation of existing solution data onto a new mesh. Data interpolation also occurs at the interface between regions, where contacting boundaries exchange data. Additionally, configurable data mappers allow you to interpolate field functions and tabular data to specified meshes.

Simcenter STAR-CCM+ interpolates solution data from a set of mesh points (source stencil) to another (target stencil). The set of points defining the source or the target stencil can include mesh vertices, cell centroids, or face centroids. For example, for a set of source surfaces with Face stencil, the source stencil comprises the centroids of all faces belonging to the source surfaces. For a set of source surfaces with Vertex stencil, the source stencil comprises all mesh vertices lying on the source surfaces.

For some cases, such as remeshing and manual data mapping, Simcenter STAR-CCM+ allows you to choose the interpolation scheme that is used to transfer data. The available interpolation schemes vary depending on the source and target stencil (face, cell, or vertex), as outlined in the following table:


		Source Stencil
		Vertex	Face	Cell
Target Stencil	Vertex	Shape Function Least Squares Nearest Neighbor	Least Squares Nearest Neighbor Conservative Enclosed Face Conservative Maximum Distance	Least Squares Nearest Neighbor
	Face	Shape Function Least Squares Nearest Neighbor	Least Squares Nearest Neighbor Exact Imprinting Approximate Imprinting	Least Squares Nearest Neighbor
	Cell	Shape Function Least Squares Nearest Neighbor	Least Squares Nearest Neighbor	Least Squares Nearest Neighbor

The following sections illustrate the shape function scheme in the context of vertex-to-face mapping. All other schemes are illustrated in the context of face-to-face mapping. The formulation can be generalized to other stencil combinations.

In all diagrams, the solution field on the blue mesh (source mesh) is interpolated to the red mesh (target mesh).

Nearest Neighbor Interpolation

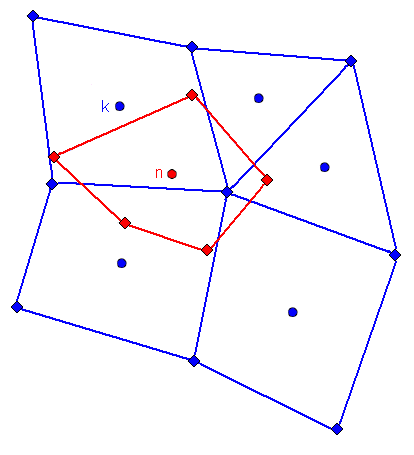
The nearest neighbor method sets the data on a target face to the data on the nearest source face. In the following diagram, the centroid of the source face k is the closest point to the centroid of the target face n. The data from face k is assigned to face n as the mapped value.

Least Squares Interpolation

The least square method uses a cost function to approximate the solution field distribution near a target location. In the following diagram, the solution field has known values

f_{i}

at the face centroids

i

on the source mesh:

To evaluate the mapped value at the target point $a$ , Simcenter STAR-CCM+ approximates the solution field $f$ using a first-order Taylor series, centered in $a$ :

Figure 1. EQUATION_DISPLAY

f (x) \approx f (x_{a}) + (x - x_{a}) \cdot \nabla f (x_{a})

(5226)

Following the least square method, Simcenter STAR-CCM+ then calculates

f (x_{a})

by minimizing the sum of squared residuals:

Figure 2. EQUATION_DISPLAY

S = \sum_{i \in F (c)}^{} {r_{i}}^{2}

(5227)

where the residuals are the differences between the values predicted by Eqn. (5226) at the source locations

i

and their known values

f_{i}

Figure 3. EQUATION_DISPLAY

r_{i} = f (x_{i}) - f_{i}

(5228)

Only the neighbors of the source face that is closest to the target face contribute to the interpolation. In Eqn. (5227), the set of centroids of the contributing faces is indicated by $F (c)$ .

In the diagram, face 0 is the closest to face a. Only the neighbors of face 0, that are defined as any face that shares at least one vertex with face 0, contribute to the interpolation. These neighbors are 2, 3, 4, 5, 6, and 8. The disadvantage is that some of the blue faces that imprint onto the target face (for example 1, 10, 11, 7) do not contribute.

Note	The least squares method is applicable to all cell types, for face and vertex source stencils.

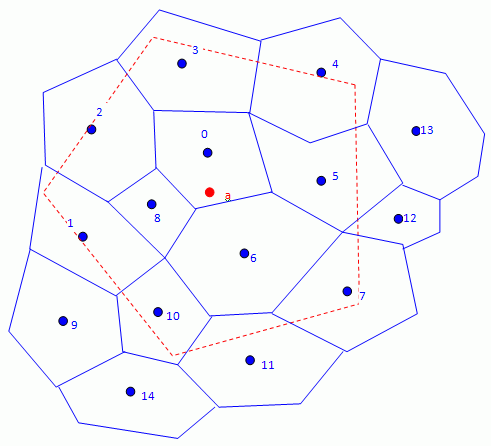
Exact Imprinting Interpolation

In the following diagram, the target face is imprinted on the source mesh. This results in several facelets that are the intersection of the source mesh (faces 0, 1, 2, 3, 4, 5, 6, 7, 8, 10, 11) with the target face a.

To evaluate the mapped value at the target point $a$ , Simcenter STAR-CCM+ uses the normalized facelet areas $A_{i}$ as interpolation weights:

Figure 4. EQUATION_DISPLAY

f_{a} A_{a} = \sum_{i \in F (c)}^{} {A_{i} f}_{i}

(5229)

$F (c)$ denotes the set of centroids $i$ of faces on the source mesh that intersect the target face. $f_{i}$ is the solution at the face centroids $i$ .

This method is preferable when:

a flux-preserving mapping is desired
the source mesh is finer than the target mesh and the surface curvature is adequately resolved

Unlike the least squares scheme, all the source faces that imprint onto the target face contribute to the interpolation.

Mapping with the exact imprint method can fail when surface curvature is inadequately resolved in either the source or target mesh.

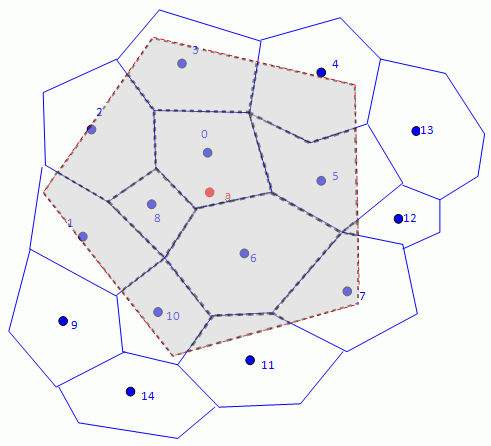
Approximate Imprinting Interpolation

This method is a variation of the exact imprinting method in which the source stencil is constructed using proximity checks instead of exact intersections. Proximity checks require less intensive computation than the exact method.

The stencil includes all source faces that lie within a circle that is centered at the target face centroid and passes through the farthest vertex of the target face. In the following diagram, the circle includes faces 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14 as part of the stencil.

Exact imprinting would eliminate faces 9, 13, and 14 from the stencil because they do not intersect the target face. As for exact imprinting, the normalized face areas are used as interpolation weights.

Although the approximate imprinting method is more robust than the exact imprinting method, it does not preserve flux quantities. The approximate method has comparable accuracy to the exact method when the source mesh is much finer than the target mesh.

Shape Function Interpolation

This interpolation method is typically used when mapping data from a finite element mesh to a finite volume mesh. In the following diagram, the solution field is known at the vertices

l

of the source mesh elements. The target face centroid n lies within the element k.

To evaluate the mapped value at the target point $n$ , Simcenter STAR-CCM+ interpolates the solution at the vertices of element k using nodal shape functions:

Figure 5. EQUATION_DISPLAY

f_{n} = {\sum_{l \in N (k)} f_{l} N_{l} (ξ_{n}, η_{n}, χ_{n})}_{}^{}

(5230)

where $N_{l}$ is the shape function at vertex $l$ , $f_{l}$ is the solution value at vertex $l$ , and ${(ξ_{n}, η_{n}, χ_{n})}_{}^{}$ denotes the local coordinates of point $n$ in the element k. The sum is over the set of vertices of element k, $N (k)$ .

The form of the nodal shape functions depends on the element type. For example, a four-node isoparametric quadrilateral in 2D has the following nodal shape functions:

Figure 6. EQUATION_DISPLAY

N_{1} = \frac{(1 - ξ) (1 - η)}{4}

(5231)

Figure 7. EQUATION_DISPLAY

N_{2} = \frac{(1 + ξ) (1 - η)}{4}

(5232)

Figure 8. EQUATION_DISPLAY

N_{3} = \frac{(1 + ξ) (1 + η)}{4}

(5233)

Figure 9. EQUATION_DISPLAY

N_{4} = \frac{(1 - ξ) (1 + η)}{4}

(5234)

Note	The shape function scheme is applicable only for triangle and quadrilateral elements in 2D and tetrahedral and hexahedral elements in 3D.

When mapping with shape functions from a finite element mesh, Simcenter STAR-CCM+ recognizes the element type and uses the relevant shape function for interpolation. Simcenter STAR-CCM+ supports quadratic elements with mid-side vertices. When mapping to a finite element mesh, however, Simcenter STAR-CCM+ only uses corner vertex values for the parametric mapping, without considering mid-side vertices.

Conservative Enclosed Face

This interpolation method is typically used when mapping data from a fine finite volume mesh to a coarse finite element mesh. The general requirement is the number of source faces is at least three times the number of target vertices.

This method marks for each target element (in red) all the source faces (in blue) with the face centroids lying inside this element. The source faces contribute to all the vertices of this element using inverse of the nodal distance method. Extra conservative constraint ensures the conservation of the physics quantities.

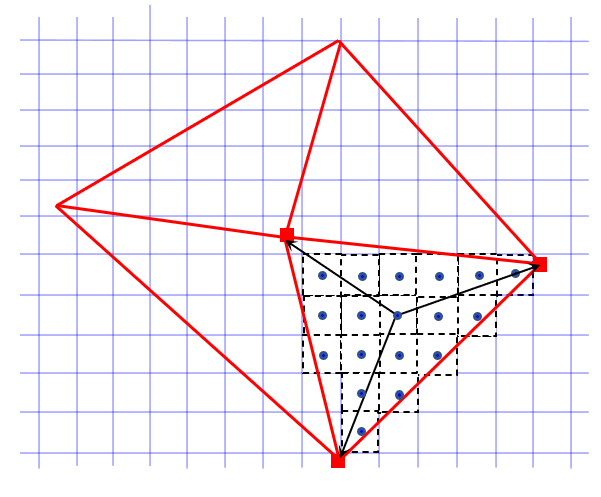
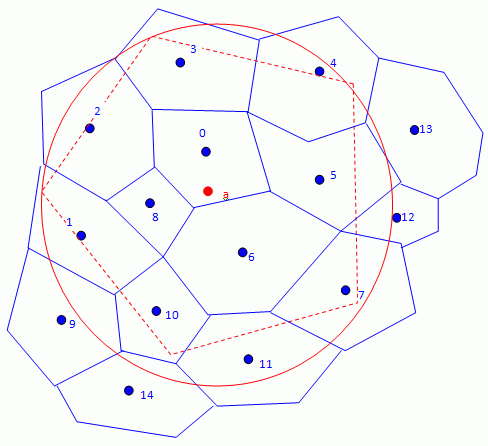
Conservative Maximum Distance

This method searches for each source face (in blue) the influencing vertices within the circle defined by Number of Influencing Nodes and Maximum Distance, as shown below:

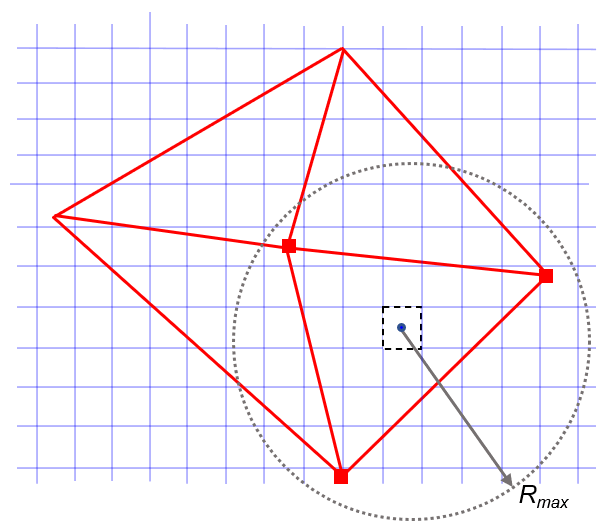
After looping on all the source faces, the mapped field on each coarse mesh vertex is computed as a weighted-sum of the solution from its influencing faces. The interpolation weights are based on rational functions of distance with conservative constraint.

Conservative Correction

Conservation correction is applied to the interpolated solution to ensure that extensive physical variables (for example, mass, momentum, total energy) are conserved after remeshing.

For mass and mass fraction the conservation equation is defined as:

Figure 10. EQUATION_DISPLAY

\sum_{i = 1}^{n_{c e l l_o l d}} ρ^{o l d} (i) \cdot y^{o l d} (i, j) \cdot v o l (i) = \sum_{k = 1}^{n_{c e l l_n e w}} ρ^{n e w} (k) \cdot y^{n e w} (k, j) \cdot v o l (k)

(5235)

where

$j$ is the species index.

$ρ^{o l d} (i)$ is the density in the $i^{t h}$ cell of the old mesh.

$y^{o l d} (i, j)$ is the mass fraction of the $j^{t h}$ species in the $i^{t h}$ cell of the old mesh.

$ρ^{n e w} (k)$ is the density in the $k^{t h}$ cell of the new mesh.

$y^{n e w} (k, j)$ is the mass fraction of the $j^{t h}$ species in the $k^{t h}$ cell of the new mesh.

and

Figure 11. EQUATION_DISPLAY

\sum_{i = 1}^{n_{c e l l_o l d}} ρ^{o l d} (i) \cdot v o l (i) = \sum_{k = 1}^{n_{c e l l_n e w}} ρ^{n e w} (k) \cdot v o l (k)

(5236)

For kinetic energy the conservation equation is defined as:

Figure 12. EQUATION_DISPLAY

\sum_{i = 1}^{n_{c e l l_o l d}} ρ^{o l d} (i) \cdot u_{o l d}^{2} (i) \cdot v o l (i) = \sum_{k = 1}^{n_{c e l l_n e w}} ρ^{n e w} (k) \cdot u_{n e w}^{2} (k) \cdot v o l (k)

(5237)

where

$u$ is the velocity component. This formula is valid for all the velocity components $u, v, w$ .

For total energy the conservation equation is defined as:

Figure 13. EQUATION_DISPLAY

\sum_{i = 1}^{n_{c e l l_o l d}} ρ^{o l d} (i) \cdot E^{o l d} (i) \cdot v o l (i) = \sum_{k = 1}^{n_{c e l l_n e w}} ρ^{n e w} (k) \cdot E^{n e w} (k) \cdot v o l (k)

(5238)

For absolute pressure, the volume conservation equation is defined as:

Figure 14. EQUATION_DISPLAY

\sum_{i = 1}^{n_{c e l l_o l d}} p^{o l d} (i) \cdot v o l (i) = \sum_{k = 1}^{n_{c e l l_n e w}} p^{n e w} (k) \cdot v o l (k)

(5239)

The total Enthalpy $H = E + p / ρ$ is conserved as a result of the conservation equations

Eqn. (5238) and Eqn. (5239).