Reacting Flow

In reacting flows, chemical species mix with each other and react when conditions allow. To model these flows, Simcenter STAR-CCM+ couples species and energy transport equations with the chemistry solvers that compute the source terms.

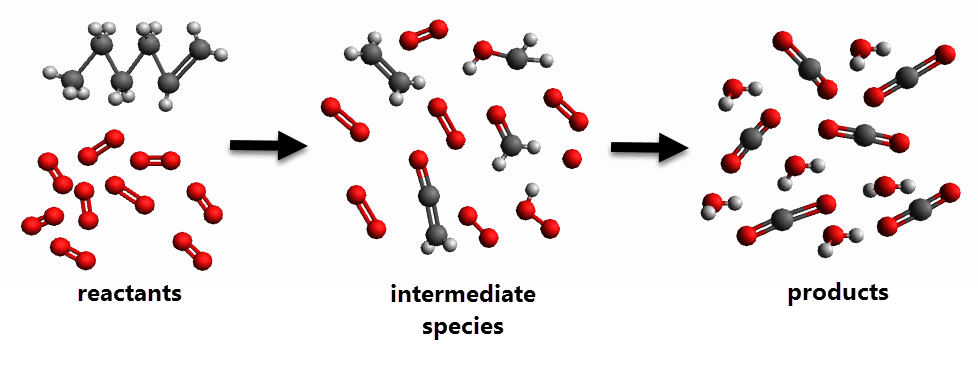
For example, the following diagram represents a reaction between a hydrocarbon (hexene) and oxygen. Often many intermediate reactions occur before the final products are created.

Examples of reacting flow systems include:

combustion in gas turbine combustors
surface reactions in aftertreatment catalysts
liquid-liquid reactions in mixing vessels
polymerization in a tubular reactor

During combustion of hydrocarbon fuels, for example, tens of thousands of reactions occur between thousands of species. Researchers develop reaction mechanisms that represent these real-life combustion scenarios in a sequence of elementary reactions. Reaction mechanisms contain anywhere from one to thousands of reactions. These reactions often have a wide variety of timescales—anywhere between $10^{- 9}$ s and $10^{2}$ s.

As an example, a simplified global reaction mechanism for propane combustion can be defined as three irreversible reactions:

C_{3} H_{8} + 1.5 O_{2} \to 3 C O + 4 H_{2}

C O + 0.5 O_{2} \to C O_{2}

H_{2} + 0.5 O_{2} \to H_{2} O

The reaction mechanism that is defined above consists of six species and three irreversible reactions. The Species transport model solves for the conservation of each of the species in this system (as described in Eqn. (1871)). The source terms that are required to close the equations are provided by the chemistry solver by utilizing the kinetic rate information that is described in the reaction mechanism. No additional chemistry-related source terms are required for the energy equation as Simcenter STAR-CCM+ solves the energy equation in chemical-thermal enthalpy form.

Modeling Approaches

Simcenter STAR-CCM+ categorizes reacting flow models into two types—reacting species transport and flamelet.

In reacting species transport models, the conservation equations, which include the chemical source term, are solved for all species in a mechanism.

The reacting species transport modeling approach is suitable for reacting flow systems in which the mixing timescale, $τ_{m i x}$ , is shorter than the reaction timescale, $τ_{k i n}$ , for one or more species. This approach is useful for simulating slowly forming pollutants, part-load conditions in combustors, and transient combustion such as explosions, ignition, and extinction.
In flamelet models, the reacting flow system is parameterized by a limited number of flamelet variables which describe the thermochemical state in the CFD cell. Instead of solving the conservation equations for all of the species, the conservation equations are solved for the limited number of flamelet variables. The number and type of flamelet variables for which the conservation equations are solved depend on the specific flamelet model. The flamelet approach has a reduced computational cost compared to the reacting species transport approach because a reduced number of transport equations are solved and the chemistry in the reaction mechanism is solved before the CFD simulation.

The flamelet modeling approach is suitable for reacting flow systems in which the reaction timescale is shorter than the mixing timescale. This approach is useful for steady-burning furnaces and burners, and full-load conditions in combustors.

In reacting flow simulations, the continuity equation and the conservation equation for flow are solved according to Eqn. (664) and Eqn. (665) respectively.

The chemical source term, $S_{i}$ , accounts for:

For reacting species transport models, the conservation equations for all species are solved using the mass fraction $Y_{i}$ of species $i$ .
For flamelet models, the conservation equations are not solved for the species mass fractions. Instead, conservation equations are solved for the relevant flamelet variables:
- mixture fraction $Z$
- mixture fraction variance $Z_{var}$
- *unnormalized progress variable $y$
- *unnormalized progress variable variance $y_{var}$
(*When using the FGM model.)
The chemical source term is also included in each progress variable conservation equation.

In Simcenter STAR-CCM+, the main difference between each of the reacting flow models is how the chemical source term

S_{i}

is formulated. Chemical reactions are exponentially dependent on temperature and successful collisions of reactants. The reaction rates depend on local instantaneous species and temperature distributions, which are not resolved in RANS and LES calculations. Therefore, different models are available to account for the fact that the average rate of reaction that is calculated for a cell does not accurately reflect the rate of reaction at specific locations within the cell. For example, differences in temperature within the cell result in species having differences in the kinetic energy that they have available for reacting.

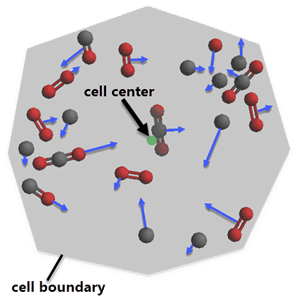
When the average reaction rate is affected by the turbulence as well as the chemistry, this phenomenon is called turbulence-chemistry interactions. Different models are used to account for these turbulence-chemistry interaction effects. Species transport models account for this effect through turbulent diffusion between cells. Time scale models can also be applied, where the time scale of the laminar chemical source term (the reaction rate calculated from average quantities) is combined with a time scale for turbulence. In flamelet models, the turbulence-chemistry interaction effects are handled through assumed shape probability density functions (PDFs) for the flamelet variables, which consider the effect of local species and temperature distributions. In addition, flame propagation models can be used to specifically model the movement of a flame front as function of turbulence and chemical state.

Reactions in Porous Media

When simulating reactions in porous media, Simcenter STAR-CCM+ defines the effective gas volume in porous regions or porous phases as follows:


Reactions in a porous region.	The effective gas volume is independent of porosity, and hence volumetric reactions are independent of the porosity.
Reactions in a phase with the Porous Media Model.	The effective gas volume is proportional to the porosity, and hence effective reaction rates are proportional to porosity.