Scalars, Vectors, and Tensors
Most physical quantities in Simcenter STAR-CCM+ are either scalars, vectors, or 2nd-order tensors.
- Scalar
- A scalar is a quantity that is completely defined by its magnitude.
- Vector
- A vector is a quantity that is completely defined by its magnitude and direction. For example, the electric field and velocity are vector quantities.
- Tensor
- A tensor is a quantity that is completely defined by its magnitude and direction on different planes of action. For example, stress and strain are tensor quantities. Like scalars and vectors, tensors can depend on other variables, such as space and time. In this case, the tensor quantity can be described using a tensor function.
Vector and Tensor Representations
As vectors and tensors are directional quantities, it is convenient to define them with respect to a coordinate system (see Coordinate Systems).
Considering the 3D Euclidean space, a vector can be written as:
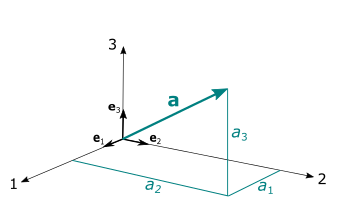
Similarly, a 2nd-order tensor can be written as:
where is the dyadic product, or tensor product, between the basis vectors (see Eqn. (5196)).
Eqn. (5184) and Eqn. (5186) are in index notation, which is also called tensor notation. The number of indices that are required to identify the tensor components define the order of the tensor. In fact, scalars and vectors can be considered as 0th-order and 1st-order tensors, respectively.
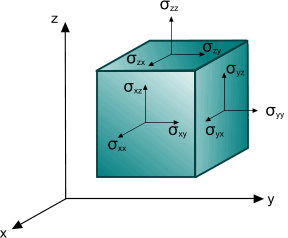
The component identifies the stress component in the direction acting on the plane normal to the axis (that is, the plane ). The component identifies the stress component in the direction acting on the plane normal to the axis (that is, the plane ).
A convenient notation consists of representing the components of vectors and tensors, with respect to a vector basis, as matrices. In matrix representation, the vector basis is implied.
In the 3D Euclidean space, the components of a vector can be represented as a one-dimensional array of length 3:
which is called the column vector representation of . The vector can also be defined using the row vector representation:
The choice of row or column representation is purely conventional. Defining row and column representations allows you to write the scalar product and the dyadic product between two vectors as matrix products (see Common Operations).
In the 3D Euclidean space, the components of a 2nd-order tensor can be represented as a 3x3 matrix:
Tensors can be defined as covariant or contravariant based on how their components transform under a change of coordinate system. This formal description is beyond the purpose of this overview.