Actual Method

Application of local heat exchanger energy sources into the hot/cold energy equations

At every solver iteration, the following steps are carried out to include the actual flow dual stream heat exchanger sources into the energy equations of the hot and cold fluid streams:

1. Solver computes the UAL Table.
2. For every cell $i$ , the mass flux ${\dot{m}}_{ci}^{"}$ entering the cell is first computed as:

   ${\dot{m}}_{ci}^{"}={\rho }_{ci}{v}_{ci}$

   where ${\rho }_{ci}$ and $v_{ci}$ are the density and magnitude of velocity of the cold stream entering the cell.

   The mass flow rate for the inlet ${\dot{m}}_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{d}}$ is computed as:

   $${\dot{m}}_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{d}}={\dot{m}}_{ci}^{"}{A}_{\mathrm{i}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{t}}$$

   where $A_{\mathrm{i}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{t}}$ is the total inlet area of the heat exchanger region through which the cold stream enters the heat exchanger. After computing ${\dot{m}}_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{d}}$, the method interpolates the UAL table to determine the local cell ${\text{ual}}_i$ corresponding to this value of ${\dot{m}}_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{d}}$.

3. For every cell $i$ of the heat exchanger region, the UAL Table is linearly interpolated to compute the local heat transfer coefficient ${ual}_i$ , given the cold and hot mass flow rates that are entering cell $i$

   If the local mass flow rate ${\dot{m}}_{\mathrm{c}\mathrm{i}}$ falls below the lowest mass flow rate ${\dot{m}}_{\min }$ in the table, then the local UAL ${\text{ual}}_i$ is extrapolated as:

   $${\text{ual}}_i={\text{ual}}_{\min }\frac{{\dot{m}}_i}{{\dot{m}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}$$

   where ${\text{ual}}_{\min }$ is the entry in the UAL table corresponding to ${\dot{m}}_{\min }$.

   If the local mass flow rate exceeds the highest mass flow rate in the table ${\dot{m}}_{\max }$, then ${\text{ual}}_i={\text{ual}}_{\max }$, where ${\text{ual}}_{\max }$ is the entry in the UAL table corresponding to ${\dot{m}}_{\max }$.

4. The local energy source is computed as:

   ${src}_i=\frac{{ual}_i\left(T_{hi}-T_{ci}\right)V_i}{\frac{1}{NC}{\sum }_{j=1}^{NC}{V}_j}$

   where:

   • $T_{hi}$ and $T_{ci}$ are the temperatures of the hot and cold streams in cell $i$
   • $V_i$ is the volume of cell $i$
   • $NC$ is the total number of cells in the heat exchanger region
5. Apply ${src}_i$ as an energy source to the cold stream energy equation and as an energy sink to the hot stream energy equation.

Computation of the UAL Table

For each entry of the user input table (UAG Table, Q Table, or Q Map), a corresponding UAL value is computed, thus generating the UAL Table.

The UAL value is computed using the following expression:

$UAL=\frac{\Gamma }{\Delta T_{net}\cdot NC}$

where

When a UAG Table is supplied:

$\mathrm{\Gamma }=UAG(T_{hot}^{inlet}-T_{cold}^{inlet})$

where:

$UAG$ is the user-table value, and $T^{inlet}$, hot or cold, is the inlet temperature for the hot or cold streams, either area averaged or mass-flow averaged over the inlet interface boundary. The summation is over all the cell faces.

• Area averaged:

  $$T^{inlet}=\frac{{\displaystyle \sum _f^{}\left[T_f{A}_f\right]}}{{\displaystyle \sum _f^{}{A}_f}}$$

  (234)

  $T_f$ and $A_f$ are the cell face values of temperature and surface area.

• Mass flow averaged:

  $$T^{inlet}=\frac{{\displaystyle \sum _f^{}[T_f{\rho }_f{\mathit{V}}_f\cdot {\mathit{A}}_f]}}{{\displaystyle \sum _f^{}[{\rho }_f{\mathit{V}}_f\cdot {\mathit{A}}_f]}}$$

  (235)

  ${\rho }_f$ and ${\mathit{V}}_f$ are the cell face values of density and velocity.

When a Q Table or a Q Map is supplied:

$\mathrm{\Gamma }=\frac{Q(T_{inlet}^{hot}-T_{inlet}^{cold})}{T_{user}^{hot}-T_{user}^{cold}}$

where:

$Q$ is the user-table value,

$T_{user}^{hot}$ and $T_{user}^{cold}$ are the user-supplied test rig inlet temperature values of the hot and cold streams respectively (these values are specified in Simcenter STAR-CCM+ as properties of Q Table or Q Map).

$\mathrm{\Delta }{T}_{net}$ is the volume averaged temperature difference between the hot and cold streams, over the exchanger region.

$\mathrm{\Delta }{T}_{net}=\frac{{\displaystyle \sum _{i=1}^{NC}{(T_{hi}-T_{ci})V}_i}}{{\displaystyle \sum _{i=1}^{NC}{V}_i}}$

Q Map Option

The Q Map option of the Actual Flow Dual Stream heat exchanger model uses bilinear interpolation to compute UAL values from an UAL map. Consider the graphical representation of a computed UAL map:

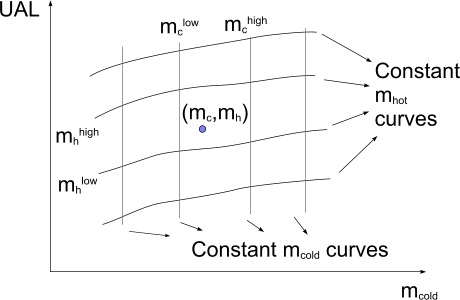
The points of intersection between the constant $m_{cold}$ and $m_{hot}$ represent data in the computed UAL map. The UAL at a general point $(m_c,m_h)$ is given by:

$UAL=u_{c1}+q_c(u_{c2}-u_{c1})$

where

$\begin{array}{c}{u}_{c1}=u_1+q_c(u_2-u_1)\\ u_{c2}=u_3+q_c(u_4-u_3)\end{array}$

and

$\begin{array}{c}{q}_c=\frac{m_c-m_c^{low}}{m_c^{high}-m_c^{low}}\\ q_c=\frac{m_h-m_h^{low}}{m_h^{high}-m_h^{low}}\end{array}$

$u_1$ , $u_2$ , $u_3$ and $u_4$ are the UAL values at points $(m_c^{low},m_h^{low})$, $(m_c^{low},m_h^{high})$, $(m_c^{high},m_h^{low})$, and $(m_c^{high},m_h^{high})$, respectively.

For example, consider the following UAL table for a given Q Map table:

The UAL for a cold mass flow rate of 1.5 kg/s and a hot mass flow rate of 5.0 kg/s is computed as:

$UAL=\frac{10+20}{2}+\left(\frac{5.0-4.0}{8.0-4.0}\right)\times [\frac{30.0-40.0}{2}-\frac{10.0+20.0}{2}]=20$