Deicing

Deicing is assumed to be a quasi-steady process.

An ice layer at temperature $T_{i c e}$ is melted with a wall heat flux $q$ , of which a proportion $C_{e m p}$ is absorbed in the ice layer. Melted ice at the freezing temperature $T_{F}$ escapes as run-off which cannot refreeze in the current model. The mass and energy fluxes that are associated with this process are illustrated in the diagram below:

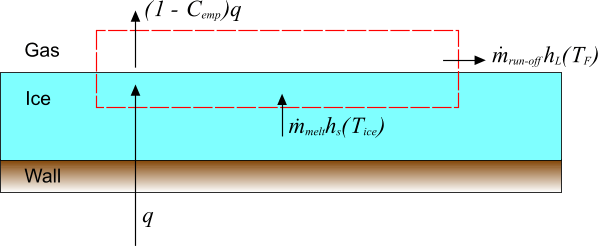
The mass balance for the deicing process is simply

Figure 1. EQUATION_DISPLAY

{\dot{m}}_{m e l t} = {\dot{m}}_{r u n - o f f}

(214)

As it is assumed that run-off cannot refreeze, there is the additional constraint that ${\dot{m}}_{r u n - o f f} \geq 0$ and hence from Eqn. (214), ${\dot{m}}_{m e l t} \geq 0$ .

The energy balance for this process, neglecting the kinetic energy that is associated with the mass fluxes, is:

Figure 2. EQUATION_DISPLAY

{\dot{m}}_{m e l t} h_{s} (T_{i c e}) + q = {\dot{m}}_{r u n - o f f} h_{L} (T_{F}) + (1 - C_{e m p}) q

(215)

where $h_{s} (T_{i c e})$ is the enthalpy of the solid ice at the temperature of the ice layer, and $h_{L} (T_{F})$ is the enthalpy that is associated with the melting ice at the freezing temperature. These enthalpies are related to temperature by:

Figure 3. EQUATION_DISPLAY

h_{s} (T) = C_{p, s} T

(216)

Figure 4. EQUATION_DISPLAY

h_{L} (T) = C_{p, s} T + L

(217)

Using these relations with the mass balance, and rearranging, gives an explicit expression for the melting rate:

Figure 5. EQUATION_DISPLAY

{\dot{m}}_{m e l t} = \frac{C_{e m p} q}{C_{p, s} (T_{F} - T_{i c e}) + L}

(218)

The constraint, ${\dot{m}}_{m e l t} \geq 0$ , must be imposed on this equation. If Eqn. (218) predicts a negative ${\dot{m}}_{m e l t}$ , it is clipped to zero.

Given ${\dot{m}}_{m e l t}$ , the ice thickness, s, can be updated using:

Figure 6. EQUATION_DISPLAY

\frac{d s}{d t} = - \frac{{\dot{m}}_{m e l t}}{ρ_{s}}

(219)

where $ρ_{s}$ is the density of the ice layer.

Accretion

The preceding analysis is extended to include an additional incident mass flux of liquid droplets, each with mass $m_{d}$ , temperature $T_{d}$ and velocity $v_{d}$ . This expression is intended to represent liquid droplets impinging on the surface. The various contributions to the overall energy balance are depicted below:

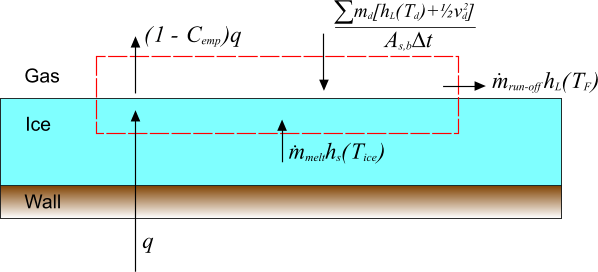
In the above diagram, $A_{s, b}$ is the surface area of the boundary face onto which the droplets impinge and $Δ t$ is the time-step. The term:

$\frac{\sum_{}^{} m_{d} [h_{L} (T_{d}) + \frac{1}{2} v_{d}^{2}]}{A_{s, b} Δ t}$

indicates the overall energy flux due to the impinging droplets.

The mass balance is therefore given as:

Figure 7. EQUATION_DISPLAY

{\dot{m}}_{m e l t} + {\dot{m}}_{d} = {\dot{m}}_{r u n - o f f}

(220)

where:

Figure 8. EQUATION_DISPLAY

{\dot{m}}_{d} = \frac{\sum_{}^{} m_{d}}{A_{s, b} Δ t}

(221)

In addition to the constraint that ${\dot{m}}_{r u n - o f f} \geq 0$ , there is also ${\dot{m}}_{d} \geq 0$ . The constraint on ${\dot{m}}_{m e l t}$ is now ${\dot{m}}_{m e l t} \geq - {\dot{m}}_{d}$ , that is, freezing is allowed but no faster than the incoming liquid rate.

The energy balance for this process is:

Figure 9. EQUATION_DISPLAY

{\dot{m}}_{m e l t} h_{s} (T_{i c e}) + \frac{\sum_{}^{} m_{d} [h_{L} (T_{d}) + \frac{1}{2} v_{d}^{2}]}{A_{s, b} Δ t} + q = (1 - C_{e m p}) q + {\dot{m}}_{r u n - o f f} h_{L} (T_{F})

(222)

giving:

Figure 10. EQUATION_DISPLAY

{\dot{m}}_{m e l t} = \frac{C_{e m p} q + \frac{\sum_{}^{} m_{d} [C_{p, s} (T_{d} - T_{F}) + \frac{1}{2} v_{d}^{2}]}{A_{s, b} Δ t}}{C_{p, s} (T_{F} - T_{i c e}) + L}

(223)

A similar analysis can be made for the accretion of solid particles.

Accretion Ratio

Following Makkonen [195], it is useful to define the accretion ratio for non-zero ${\dot{m}}_{d}$ as:

Figure 11. EQUATION_DISPLAY

α = - \frac{{\dot{m}}_{m e l t}}{{\dot{m}}_{d}}

(224)

This quantity characterizes the nature of the accretion process. When $α = 1$ there is no run-off and the accretion is “dry”, which tends to form rime ice. Otherwise there is some run-off, and the “wet” growth tends to form glaze ice. The accretion ratio is sometimes also known as the “freezing fraction”.