Examples of Setting Porous Resistance Properties

Porous resistance properties can be specified in several different ways depending on the characteristics of the porous media being modeled and the expected flow conditions through it.

By making it possible to specify porous resistances using field functions and expressions (as well as constant values), Simcenter STAR-CCM+ provides a framework whereby you can define your own resistance models. This section provides some examples of how to do this.

Orthotropic Viscous Resistance

Consider a tube bundle of the type often used to condition flows in pipes and ducts. This porous medium is situated in a section of the duct that is oriented at 45 degrees to the x-axis as shown below.

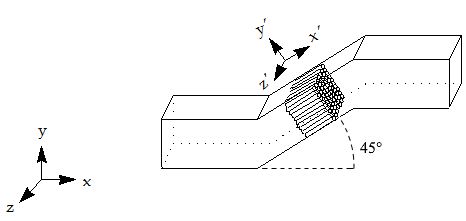
Measurements undertaken in a wind tunnel (air is the working fluid) have shown that the tube bundle device imparts a pressure drop of 70 Pa per meter when the velocity is 1 m/s. In addition, for the range of velocities of interest, the pressure drop varies linearly with velocity.

Since the Reynolds number is low, only the viscous resistance tensor $P_{v}$ is specified, so the porous resistance is a linear function of flow velocity. In the orthotropic coordinates, the primary coefficient is 70. To restrict the flow in the directions perpendicular to the primary direction, choose a resistance coefficient that is 2-3 orders of magnitude larger than primary coefficient, for example 10000. Choosing a larger resistance does not affect the flow but can adversely affect the convergence characteristics. Therefore the viscous resistance tensor in orthotropic coordinates is chosen to be:

[\begin{matrix} 70 & 0 & 0 \\ 0 & 10000 & 0 \\ 0 & 0 & 10000 \end{matrix}]

This tensor can be specified in Simcenter STAR-CCM+ using the orthotropic tensor profile method: The XX, YY and ZZ components are 70, 10000 and 10000 respectively. Orientation Manager > [local orientation] > Principle Axis 1 is the vector (1, 1, 0) relative to the Laboratory Coordinate System, representing a vector that is tilted at 45 degrees to the Laboratory x-axis. Principle Axis 2 is then (-1, 1, 0), also relative to the Laboratory coordinate system.

Isotropic Resistance Using the Ergun Equation (Forchheimer for Packed Beds)

One of the classic equations describing flow through a porous medium is Darcy’s law, which relates the flow velocity to the pressure gradient based on a measure of permeability. This law, which applies to creeping flow ( $Re ≪ 1$ ), is expressed using [425] as:

Figure 1. EQUATION_DISPLAY

- \nabla p = \frac{μ}{k_{p}} v_{s}

(237)

where $μ$ is the fluid molecular viscosity, $k_{p}$ is the permeability (considered to be an intrinsic property of the porous medium) and $v_{s}$ is the superficial velocity through the medium.

As the flow velocity increases, the relationship between velocity and pressure gradient becomes nonlinear. Dupuit and Forchheimer (as reported by [425]) proposed the addition of a quadratic term as follows:

Figure 2. EQUATION_DISPLAY

- \nabla p = \frac{μ}{k_{p}} v_{s} + b ρ | v_{s} | v_{s}

(238)

Eqn. (238) is commonly known as the Forchheimer equation [425]. The factor $b$ must be deduced depending on the particular flow and medium of interest and is commonly determined through experiment.

One example of the Forchheimer equation for a particular class of flow is the Ergun equation (as discussed in [156]). This equation is an empirical model for the pressure drop $d p$ over a length $L$ of fluid flowing through a packed bed:

Figure 3. EQUATION_DISPLAY

- \frac{d p}{L} = P_{v} + P_{i} = \frac{150 μ {(1 - χ)}^{2} v_{s}}{χ^{3} {D_{p}}^{2}} + \frac{1.75 ρ (1 - χ) v_{s}^{2}}{χ^{3} D_{p}}

(239)

where:

$P_{v}$ and $P_{i}$ are the viscous and internal terms.
$ρ$ is the fluid density.
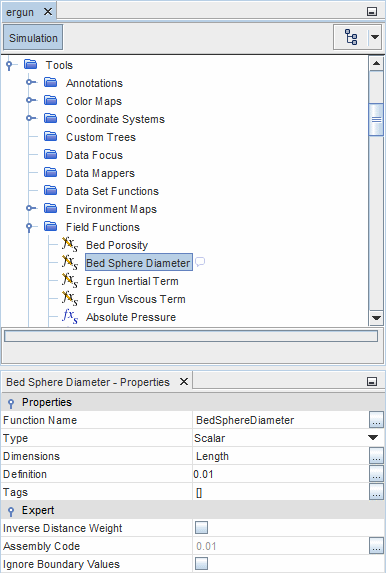
$D_{p}$ is the mean diameter of particles in the porous medium.
$χ$ is the volume porosity.

Comparing Eqn. (239) with Eqn. (238) shows that the permeability and $b$ factor are:

Figure 4. EQUATION_DISPLAY

\frac{1}{k_{p}} = \frac{150 {(1 - χ)}^{2}}{χ^{3} {D_{p}}^{2}}

(240)

and

Figure 5. EQUATION_DISPLAY

b = \frac{1.75 (1 - χ)}{χ^{3} D_{p}}

(241)

To implement this model in Simcenter STAR-CCM+, it is necessary to create user field functions for each of these terms. Field functions are first defined for the volume porosity and mean particle diameter (which are set to constant values in this example). These values are then used in the field functions for the two terms.

Parameter Field Functions

The volume porosity is defined as a scalar field function with no dimensions, and whose Definition is set to the required value (0.39 in this example).

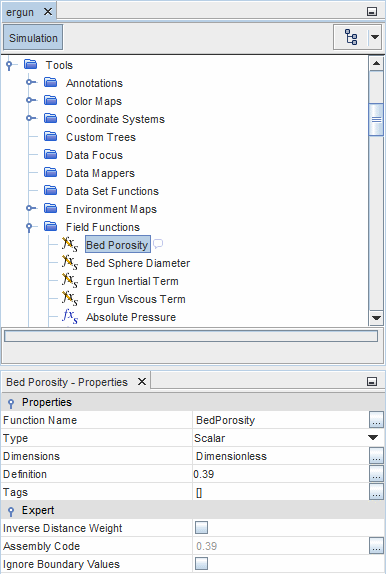
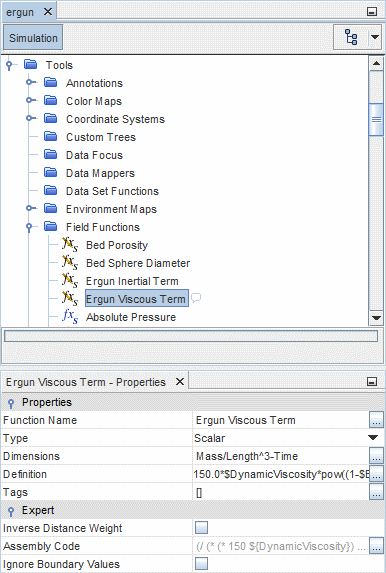
The particle diameter (0.01 m in this example) is defined in a similar way, except that the Dimensions property is set to Length.

Viscous Term Field Function

The scalar field function for the viscous term is dimensioned as

M a s s \cdot L e n g t h^{- 3} \cdot T i m e^{- 1}

, and the full Definition is:

150.0*$DynamicViscosity*pow((1-$BedPorosity),2)/(pow($BedPorosity,3)*pow($BedSphereDiameter,2))

The function uses the Bed Porosity and Bed Sphere Diameter functions that were defined previously.

This field function is applied to the Porous Viscous Resistance node as an isotropic tensor.

Select the Physics Values > Porous Viscous Resistance node on the porous region.
In the Properties window, set the Method to Isotropic Tensor using the drop-down menu. The Isotropic Tensor child node is shown underneath the Porous Viscous Resistance node.
Select the Isotropic Tensor > Isotropic Component node and, in the Properties window, set the Method to Field Function.
Finally, edit the Scalar Function property and choose Ergun Viscous Term.

Inertial Term Field Function

The scalar field function for the inertial term is dimensioned as

M a s s \cdot L e n g t h^{- 4}

, and the Definition is:

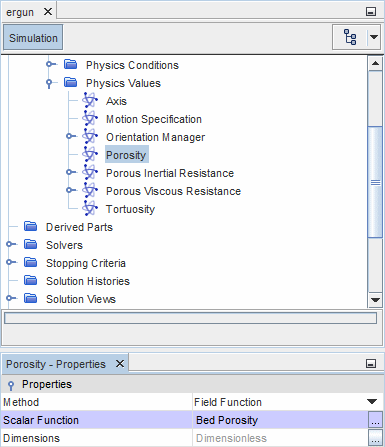
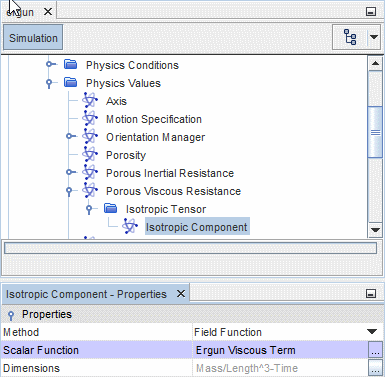
(1.75*$Density*(1-$BedPorosity))/ (pow($BedPorosity,3)*$BedSphereDiameter)

The fluid density is included in this field function. Any variations in the fluid density therefore affect the inertial resistance. This function is applied to the Porous Inertial Resistance using the isotropic tensor method as before:

Region Porosity

For an unsteady calculation, the volume porosity

χ

can be set on the region using the Bed Porosity field function. To set the volume porosity:

Select the Physics Values > Porosity node of the porous region.
In the Properties window, set the Method property to Field Function using the drop-down menu, then set the Scalar Function property to Bed Porosity.