Bulk Boiling

The Mixture Multiphase (MMP) bulk boiling model in Simcenter STAR-CCM+ models boiling and condensation in the interior of the flow.

The rate of mass transfer between the phases depends only on the heat transfer rate from the liquid and vapor to a saturated interface between these two phases. It is important that the interfacial area density is provided by a well-defined characterization of bubbles by their size and number density.

This thermally driven model is not suitable for describing boiling without bubbles (homogeneous nucleation), evaporation (concentration-driven multi-component mass transfer), nor cavitation (inertially limited mass transfer). It is also not suitable when the resulting interphase mass transfer rate occurs on time scales that are much shorter than flow time scales. This scenario is unlikely to be solvable with a segregated solver algorithm.

The heat transfer from the phase-change interface to each of the two phases on either side of the interface is modeled as:

Figure 1. EQUATION_DISPLAY

Q_{i}^{(i j)} = h_{i}^{(i j)} a_{i j} (T_{i j} - T)

(2909)

Q_{j}^{(i j)} = h_{j}^{(i j)} a_{i j} (T_{i j} - T)

where:

$T$ is the bulk temperature of the mixture.
$T_{i j}$ is the interface temperature (saturation temperature).

The interface temperature is often defined as a constant saturation temperature for a particular system pressure. In Simcenter STAR-CCM+, a field function can optionally be used for the interface temperature, so that depth can be accounted for, or overpressure due to surface tension in micron-sized bubbles.

The heat transfer coefficient for energy supply from the continuous phase is:

Figure 2. EQUATION_DISPLAY

h_{i}^{(i j)} = N u_{i} k_{i} / l_{i j}

(2910)

where $N u_{i}$ is the continuous phase Nusselt number and $l_{i j}$ is the interaction length scale for the phase pair, usually the bubble size.

Similarly, for the dispersed phase, the heat transfer coefficient for energy supply is:

Figure 3. EQUATION_DISPLAY

h_{j}^{(i j)} = N u_{j} k_{j} / l_{i j}

(2911)

where $N u_{j}$ is the dispersed phase Nusselt number.

The Nusselt number of the continuous phase is calculated using the Eqn. (2043). This correlation is not available for the dispersed phase Nusselt number since convective processes are often defined poorly inside the particle.

In a multiple flow regime phase interaction, a typical scenario for bulk boiling/condensation is shown below:

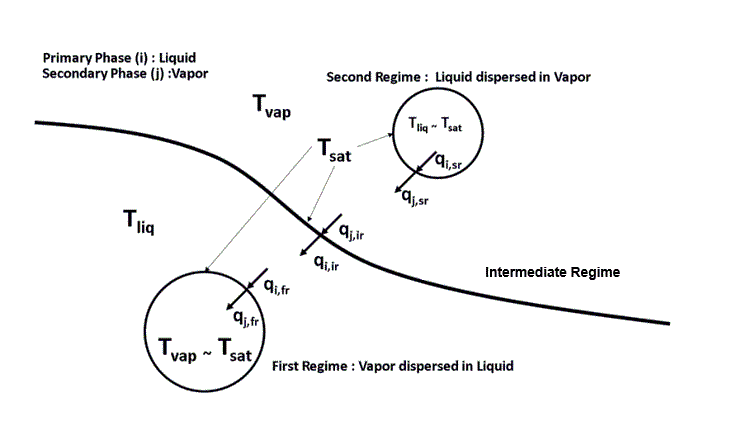
The heat transfer is calculated for a total of six situations for a pair of primary phase ( $i$ ) and secondary phase ( $j$ ). That is, for each regime, the heat transfer from a phase to the interface is calculated. The heat-transfer coefficient for the energy supply from the primary phase and secondary phase is the weighted sum of the heat-transfer coefficient at the interface for the first dispersed regime, the intermediate regime, and the second dispersed regime:

Figure 4. EQUATION_DISPLAY

h_{i}^{(i j)} a_{i j} = \sum_{r = f r, i r, s r} W_{r} (h_{i, r}^{(i j)} a_{i j, r})

(2912)

Figure 5. EQUATION_DISPLAY

h_{j}^{(i j)} a_{i j} = \sum_{r = f r, i r, s r} W_{r} (h_{j, r}^{(i j)} a_{i j, r})

(2913)

In the above equations, the primary and secondary side heat transfer coefficient for different regimes is calculated as:

For the primary (liquid) side:
- first dispersed regime, $h_{i, f r} = {N u}_{i, f r} \frac{k_{i}}{l_{f r}}$
- intermediate regime $h_{i, i r} = {N u}_{i, i r} \frac{k_{i}}{l_{i r}}$
- second dispersed regime $h_{i, s r} = {N u}_{i, s r} \frac{k_{i}}{l_{s r}}$
For the secondary (vapor) side:
- first dispersed regime, $h_{j, f r} = {N u}_{j, f r} \frac{k_{j}}{l_{f r}}$
- intermediate regime $h_{j, i r} = {N u}_{j, i r} \frac{k_{j}}{l_{i r}}$
- second dispersed regime $h_{j, s r} = {N u}_{j, s r} \frac{k_{j}}{l_{s r}}$

Note

In the first and second dispersed regime, there can be specific situations when high convective currents are not expected within the spherical body. In these situations, the bubbles and droplets can be treated as lumped bodies. To ensure that there is a uniform temperature within the spherical body (that is, the vapor side for the first dispersed regime and the liquid side for the second dispersed regime), the Nusselt number is calculated using the corresponding fluid properties as $\frac{h_{i n t e r n a l} \cdot l}{k}$ , where $h_{i n t e r n a l} = \frac{ρ \cdot c p \cdot l}{Δ t_{s}}$ . $Δ t_{s}$ is the relaxation time-scale to ensure rapid equalization of temperature, and can be set to a low value, for example, $Δ t_{s} = 1 e^{- 5} s$ .

Hughes and Duffey Correlation

The liquid side heat transfer coefficient in the intermediate regime is calculated using the surface renewal theory that is introduced by Hughes and Duffey ([478]). The Nusselt number predicted by this theory is:

Figure 6. EQUATION_DISPLAY

{N u}_{i, i r} = \frac{2}{\sqrt{π}} {Re}_{t} \Pr_{i}^{1 / 2}

(2914)

where:

${Re}_{t} = l_{t} u_{t} / ν_{l}$ is the turbulent Reynolds number
- $l_{t}$ is the turbulent length scale
- $u_{t}$ is the turbulent velocity scale
- $ν_{l}$ is the liquid kinematic viscosity.
$P_{r l}$ is the liquid Prandtl number.

This method is available only when the primary phase is a turbulent model.

The interface mass flux is computed from the heat balance:

Figure 7. EQUATION_DISPLAY

m^{(i j)} = - \frac{Q_{i}^{(i j)} + Q_{j}^{(i j)}}{{Δ h}_{i j}}

(2915)

where:

$m^{(i j)}$ is the signed mass transfer rate per unit interfacial area for the interaction from phase j to phase i
${Δ h}_{i j}$ is the signed enthalpy input to create phase j from phase i