Eulerian: Suspension Rheology

This tutorial demonstrates how to set up a Simcenter STAR-CCM+ simulation that models the flow of a non-Newtonian concentrated suspension.

In this tutorial, you simulate the low Reynolds number rotating shear flow of a suspension of neutrally buoyant monodisperse particles in a Newtonian liquid through a Couette device. The simulation predicts the velocity field, the particle volume fraction, and the particle phase pressure. The geometric dimensions, the rotational speed, and the material properties correspond to the experimental investigations by Philips and others [978]. The simulation results are compared with experimental values from the paper.

The Phillips experiment measured the spatial variation of the particle volume fraction that was caused by particle migration in the rotating flow. Particles in a suspension tend to migrate from regions of high shear rate towards regions of lower shear rate: in the Couette device, the particles moved away from the rotating wall.

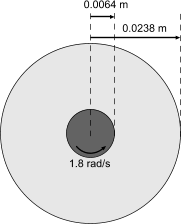
The geometry that is used in this simulation is a circular 2D cross section of a Couette device. The inner wall of the Couette device, with a radius of 0.64 cm, rotates at an angular velocity of 1.8 rad/s, which corresponds to a rotation rate of approximately 17 rpm. The outer wall has a radius of 2.38 cm and remains fixed.

The computational domain is filled with Polymethylmethacrylate (PMMA) spherical particles of density 1182 kg-m⁻³ suspended in a Newtonian tetrabromoethane/oil mixture with the same density as the particles and a dynamic viscosity of 4.95 Pa-s. The mean particle diameter is 0.001 meters and the initial volume fraction of particles is 0.55.

The geometry is resolved by a hexahedral mesh with 1600 cells. The flow of the suspension is modeled by the Eulerian Multiphase approach. The rheological description of the suspension is provided by the Morris and Boulay model. This model goes beyond considering purely shear viscosity and takes into account the normal stress contributions that cause the shear induced migration of particles in the flow.

In suspension rheology, the dimensionless relative (effective) viscosity is used to describe the mixture viscosity. The mixture viscosity increases with particle volume fraction, as more particles interact with each other, along with the hydrodynamic forces in the fluid between the particles. As the mixture approaches maximum packing of the particles, networks of contact form between the particles and the mixture jams [973], so the relative viscosity tends to infinity.

In the Morris and Boulay model, the relative viscosity is defined as:

Figure 1. EQUATION_DISPLAY

η_{r} (ϕ) = 1 + 2.5 ϕ {(1 - \frac{ϕ}{ϕ_{m}})}^{- 1} + K_{s} {(\frac{ϕ}{ϕ_{m}})}^{2} {(1 - \frac{ϕ}{ϕ_{m}})}^{- 2}

(5253)

where $K_{s}$ is the shear contact contribution and $ϕ_{m}$ is the maximum packing fraction.

The dependence of the compressive shear-induced normal stresses on the particle volume fraction $ϕ$ is captured by a normal relative viscosity $η_{n} (ϕ)$ which is defined as:

Figure 2. EQUATION_DISPLAY

η_{n} (ϕ) = K_{n} {(\frac{ϕ}{ϕ_{m}})}^{2} {(1 - \frac{ϕ}{ϕ_{m}})}^{- 2}

(5254)

where $K_{n}$ is the normal contact contribution.

In this simulation, the normal relative viscosity is equivalent to an isotropic particle pressure that causes the particles to migrate towards regions of low shear-rate.

This simulation uses a maximum packing volume fraction $ϕ_{m}$ of the suspension of 0.68. This value is higher than the theoretical monodisperse value of random close packing, which is around 0.645, in order to reflect the polydispersity of the particles.