Impingement

Liquid droplets can impinge on a dry wall to form a fluid film or they can impinge on an existing fluid film, a free surface given by a Volume-of-Fluid (VOF) phase. In both cases, the mass, the momentum, and the energy of the droplets are transferred to the film.

Fluid Film Impingement

Droplets that reach the free-surface between the continuous phase and a liquid film can be set to impinge onto the liquid film. All of the particle mass, energy, and momentum are transferred to the liquid film.

The mass that is transferred due to impingement of a dispersed DMP phase $i$ acts as a mass source to the liquid film, and is calculated as:

Figure 1. EQUATION_DISPLAY

{\dot{m}}_{imp} = ρ_{i} v_{i} \cdot a_{fs}

(2858)

where:

${\dot{m}}_{imp}$ is the impinging mass flux of the dispersed DMP phase
$ρ_{i}$ is the density of the dispersed phase
$a_{fs}$ is the area vector of the free surface

Corresponding sources are also applied to the momentum and energy transport equations.

Volume-of-Fluid (VOF) Phase Impingement

When two-way coupling is activated, a DMP phase can impinge onto the surface of a VOF phase or a wall. Only a fraction of the impinging mass, momentum, and energy fluxes of the dispersed DMP phase are transferred to the VOF phase.

The following diagram depicts a situation where a droplet, modelled as DMP phase, impinges on the free surface of a liquid, modelled as VOF phase, or on a dry wall. Mass of an impinging DMP phase is transferred only to a VOF phase of the same material as the DMP phase. The cell through which the droplet approaches the free surface is not entirely filled with the blue VOF phase, the portion of fill given by the volume fraction $α_{VOF}$ .

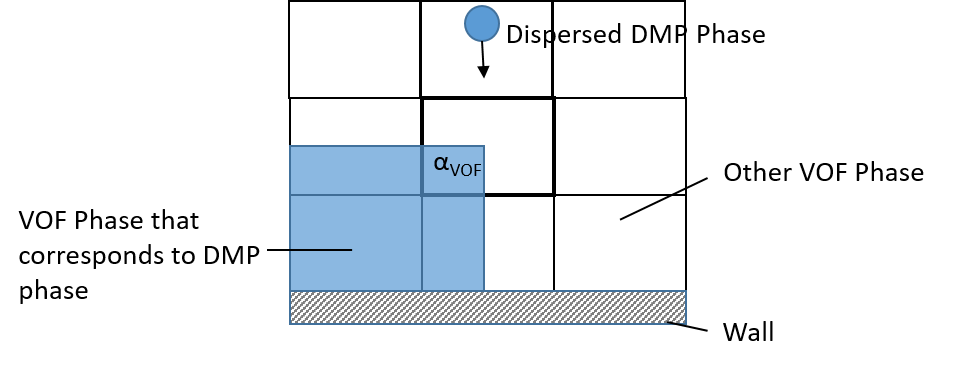
Free Surface Impingement

When a DMP phase impinges on a free surface, the mass transferred to the VOF phase due to impingement is calculated as:

Figure 2. EQUATION_DISPLAY

{\dot{m}}_{VOF} = α_{VOF} \cdot {\dot{m}}_{imp}

(2859)

where:

${\dot{m}}_{VOF}$ is the mass source to the VOF phase
${\dot{m}}_{imp}$ is the impinging mass flux of the DMP phase
$α_{VOF}$ is the volume fraction of the VOF phase

The fraction equals the volume fraction of VOF phase $α_{VOF}$ in the cell as it is a measure of the collision probability between the DMP phase and the VOF phase.

Wall Impingement

When a DMP phase impinges on a wall, and the cell is partially filled with VOF phase, the mass flux transferred to the wall due to impingement is calculated as:

Figure 3. EQUATION_DISPLAY

{\dot{m}}_{wall} = (1 - α_{VOF}) \cdot {\dot{m}}_{imp}

(2860)

The DMP phase hitting the wall is transformed into the VOF phase of the same material as the DMP phase. The incoming DMP mass flux on the wall is calculated by taking only the normal component of the DMP velocity to the wall.

Corresponding sources are also applied to the momentum and energy transport equations.