Broadband Noise Source Models

For near-field prediction, Simcenter STAR-CCM+ offers a group of models capable of evaluating the broadband sources of noise. The noise sources consist of a volume distribution of quadrupole sources and a surface distribution of dipole sources.

In the frequency domain, a broadband noise has a continuous spectrum, where the acoustic energy is continuously distributed at all frequencies in a given range. These models calculate the location and strength of the main sources of noise that are generated aerodynamically. They use flow field quantities from Reynolds-Averaged Navier-Stokes (RANS) Turbulence equations. Because these broadband noise models use RANS simulations, the required computational time is small.

The following broadband noise source models perform the following operations on the local acoustic power:

Curle noise source model: estimates the sound per unit surface generated by dipole sources
Goldstein axisymmetric noise source model
Proudman noise source model: estimate the sound per unit volume generated by quadrupole sources
Lilley noise source model
Linearized Euler Equation (LEE) noise source model: estimate the sound generated by turbulent shear flow
Stochastic Noise Generation and Radiation (SNGR) model: computes a synthetic turbulence field
Lighthill stress tensor: estimates noise sources generated by flow
Acoustic Suppression Zone model: suppresses spurious reflections
Mesh frequency cutoff analysis: checks if the grid is fine enough to resolve turbulent flow structures of interest

The decomposition of the main sources of aerodynamically generated sound can be done onto a shear noise term, representing the interaction between the mean shear velocities and turbulent velocity components of the flow, and the self-noise term, representing turbulence-turbulence interactions.

Speed of Sound

The far-field speed of sound $c_{0}$ is the distance that a sound wave travels in a unit of time.

Figure 1. EQUATION_DISPLAY

c_{0} = \sqrt{(γ {R T}_{0})}

(4659)

where:

$γ$ is the adiabatic index or the ratio of heat capacity at constant pressure to the heat capacity at constant volume for the fluid.
$R$ is the universal gas constant
$T_{0}$ is the absolute temperature, measured in Kelvin.

In dry air at 293 K, the speed of sound is 343.2 m/s.

Curle Noise Source Model

The Curle Noise Source model evaluates the noise from a turbulent boundary layer flow over a solid body, assuming isotropic turbulence and low Mach numbers.

This model is typically used for air-handling subsystem (AHS) applications, including rotating parts (such as blowers), heat exchangers, mufflers, distribution ducts, and wall-enclosed spaces.

The Curle model represents dipole sources of noise, that is, noise coming from the fluctuating surface pressure that results from solid boundaries acting on the fluid. Specifically, this model calculates the local contribution to the acoustic power per unit area of body surface.

Following Curle [884], the acoustic density can be written in terms of the local contributions as:

Figure 2. EQUATION_DISPLAY

ρ′ (x, t) = \frac{1}{(4 π c_{0}^{3})} \int_{S}^{} [\frac{(x - y)}{r^{2}} \frac{\partial p}{\partial t} (y, t - \frac{r}{c_{0}})] \cdot n d S (y)

(4660)

where:

$ρ'$ is the acoustic density.
$c_{0}$ is the far-field sound speed.
$t - \frac{r}{a_{0}}$ is the emission time.
$p$ is the surface pressure.
$x$ is the position in the far-field, where $| x | ≫ λ$ and $λ$ is the typical wavelength of the sound generated, so that $x$ lies in the radiation field of each dipole noise source.
$y$ is the face centroid position on the solid boundary surface.
$r = | x - y |$ is the physical distance between the source and far-field positions.
$n$ is the outward wall-normal direction.

On the assumption of small perturbations and an adiabatic problem:

Figure 3. EQUATION_DISPLAY

\frac{p}{ρ^{γ}} = const

(4661)

where $γ$ is the ratio of specific heats at constant pressure ( $C_{P}$ ) and constant volume ( $C_{V}$ ).

Respecting isentropy for the perturbation, the variation of the acoustic pressure and density perturbations can be written as:

Figure 4. EQUATION_DISPLAY

p′ = c_{0}^{2} ρ′

(4662)

Then Eqn. (4660) for acoustic density becomes the following equation for acoustic pressure:

Figure 5. EQUATION_DISPLAY

p′ (x, t) = \frac{1}{(4 π c_{0})} \int_{S}^{} [\frac{(x - y)}{r^{2}} \frac{\partial p}{\partial t} (y, t - \frac{r}{c_{0}})] \cdot n d S (y)

(4663)

In the far field, the acoustic directional intensity along $x - y$ , per unit surface of the solid body surface, is approximated with:

Figure 6. EQUATION_DISPLAY

\bar{{p^{'}}^{2}} \approx \frac{1}{16 π^{2} c_{0}^{2}} \int_{S}^{} \frac{{(\cos θ)}^{2}}{r^{2}} \bar{{[\frac{\partial p}{\partial t} (y, t - \frac{r}{c_{0}})]}^{2}} A_{c} (y) d S (y)

(4664)

where:

$A_{c}$ is the acoustic correlation area.
$θ$ is the angle between $r$ and the wall-normal $n$ , so that $| x - y | \cdot n = r \cos (θ)$

The measure of the local contribution to acoustic power per unit surface, Surface Acoustic Power or SAP, can be computed from:

Figure 7. EQUATION_DISPLAY

S A P = \frac{1}{ρ_{0} c_{0}} [\int_{0}^{2 π} \int_{0}^{π} \overline{{p′}^{2}} r^{2} \sin θ d θ d γ]

(4665)

Then the Surface Acoustic Power can be calculated from:

S A P = \frac{1}{12 π ρ_{0} c_{0}^{3}} \int_{S}^{} \bar{{(\frac{\partial p}{\partial t})}^{2}} A_{c} (y) d S (y)

The relation can be rewritten to include the acoustic correlation area formulation and the mean-square time derivative of the surface pressure $\bar{{(\partial p / \partial t)}^{2}}$ as:

S A P = \frac{1}{12 π ρ_{0} c_{0}^{3}} \cdot 4 π^{3} \bar{{({u^{'}}_{turb})}^{2}} {({p^{'}}_{wall})}^{2}

where for ${p^{'}}_{wall}$ and $\bar{{({u^{'}}_{turb})}^{2}}$ Hinze[896] gives:

{p^{'}}_{wall} = max (3 τ_{wall}, 0.7 ρ_{0} \cdot \frac{2}{3} k)

and

\bar{{({u^{'}}_{turb})}^{2}} = \frac{2}{3} max (k, \frac{3.3 τ_{wall}}{ρ_{0}})

${p^{'}}_{wall}$ is wall pressure fluctuation.
$\bar{{({u^{'}}_{turb})}^{2}}$ is the mean square turbulent velocity.
$k$ is the turbulent kinetic energy.
$τ_{wall}$ is the wall shear stress.
$ρ_{0}$ is the far-field density.

The Curle model can be activated for steady and unsteady simulations with Reynolds-Averaged Navier-Stokes (RANS) turbulence models, which provide turbulence kinetic energy and wall shear stress.

The acoustic power per unit surface can be reported in dimensional units ( ${W/ m}^{2}$ ) and in dB:

Figure 8. EQUATION_DISPLAY

S A P (dB) = 10 \log \frac{S A P}{P_{ref}}

(4666)

where $P_{ref}$ is the reference acoustic power.

Goldstein Axisymmetric Noise Source Model

The Goldstein model is based on Lighthill's theory for predicting aerodynamic noise from a turbulent shear flow on an assumption of locally homogeneous and anisotropic turbulence.

Goldstein [895] generalizes Ribner's model [910] for axisymmetric turbulent flow by eliminating Ribner's assumption of the space-time correlations of Reynolds stresses.

This model computes the local noise contribution per unit volume for anisotropic turbulence in axisymmetric turbulent jets.

The local contribution to the total acoustic power per unit cell volume is computed from:

Figure 9. EQUATION_DISPLAY

G_{A P} (y) = \int_{0}^{2 π} \int_{0}^{π} {I (r, θ / y) r}^{2} \sin (θ) d θ d γ = 2 π r^{2} \int_{0}^{π} I (r, θ / y) \sin (θ) d θ

(4667)

where $r$ and $θ$ are the radial and angular coordinates of the receiver location, with the receiver assumed to be sufficiently far away from the flow. $I (r, θ / y)$ is the directional acoustic intensity per unit volume of a jet:

Figure 10. EQUATION_DISPLAY

I (r, θ / y) = \frac{{12 ρ}_{0} {ω_{f}^{4} L}_{1} L_{2}^{2} {(\overline{u_{t l}^{2}})}^{2}}{5 π c_{0}^{5} r^{2}} \frac{D_{self}}{C^{5}} + \frac{{24 ρ}_{0} {ω_{f}^{4} L}_{1} L_{2}^{4} (\overline{u_{t l}^{2}})}{π c_{0}^{5} r^{2}} {(\frac{\partial U}{\partial r})}^{2} \frac{D_{shear}}{C^{5}}

(4668)

$C$ is the modified convection factor:

Figure 11. EQUATION_DISPLAY

C = 1 - M_{c} (\cos θ)

(4669)

The decomposition of the sound intensity into shear and self-noise (with no coupling terms) occurs under the assumption that turbulence is locally homogeneous:

Figure 12. EQUATION_DISPLAY

I (r, θ / y) = I_{self} (r, θ / y) + I_{shear} (r, θ / y)

(4670)

Figure 13. EQUATION_DISPLAY

I_{self} (r, θ / y) = \frac{{12 ρ}_{0} {ω_{f}^{4} L}_{1} L_{2}^{2} {(\overline{u_{t l}^{2}})}^{2} D_{self}}{5 π c_{0}^{5} r^{2} C^{5}}

(4671)

Figure 14. EQUATION_DISPLAY

I_{shear} (r, θ / y) = \frac{{24 ρ}_{0} {ω_{f}^{4} L}_{1} L_{2}^{4} (\overline{u_{t l}^{2}}) v_{grad}^{2} D_{shear}}{π c_{0}^{5} r^{2} C^{5}}

(4672)

where:

$ρ_{0}$ is the far-field density.
$c_{0}$ is the far-field speed of sound.
$v_{grad} = \frac{\partial U}{\partial r}$

Figure 15. EQUATION_DISPLAY

D_{self} = 1 + 2 (\frac{M}{9} - N) {cos}^{2} θ {sin}^{2} θ + \frac{1}{3} [\frac{M^{2}}{7} + M - 1.5 N (3 - 3 N + \frac{1.5}{Δ^{2}} - \frac{Δ^{2}}{2})] {sin}^{4} θ

(4673)

Figure 16. EQUATION_DISPLAY

D_{shear} = {cos}^{2} θ [{cos}^{2} θ + \frac{1}{2} (\frac{1}{Δ^{2}} - 2 N) {sin}^{2} θ]

(4674)

The effect of the anisotropic structure of the turbulence appears through the following parameters:

Figure 17. EQUATION_DISPLAY

\begin{matrix} M = {[\frac{3}{2} (Δ - \frac{1}{Δ})]}^{2} N = 1 - \frac{(\bar{u_{t 2}^{2}})}{(\overline{u_{t 1}^{2}})} Δ = \frac{L_{2}}{L_{1}} \\ L_{1} = \frac{{(\overline{u_{t 1}^{2}})}^{\frac{3}{2}} T^{3}}{L^{2}} L_{2} = \frac{{(\overline{u_{t 2}^{2}})}^{\frac{3}{2}} T^{3}}{L^{2}} ω_{f} = 2 π (\frac{1}{T}) \end{matrix}

(4675)

where $L_{1}$ and $L_{2}$ are the longitudinal and transverse correlation lengths, which are not equal. The longitudinal and transversal turbulence velocities $\overline{u_{t 1}^{2}}$ and $\overline{u_{t 2}^{2}}$ are not equal in all directions, so $N \neq 0$ and $Δ \neq 1$ . In the limiting case of isotropic turbulence the directivity expressions become identical to those of the Ribner model, so $N = M = 0$ and $Δ = 1$ .

The longitudinal and transverse turbulence velocities $\overline{u_{t 1}^{2}}$ and $\overline{u_{t 2}^{2}}$ are computed using the following relations:

Figure 18. EQUATION_DISPLAY

\begin{matrix} \overline{u_{t 1}^{2}} = \frac{8}{9} (\frac{L^{2}}{T^{2}}) \overline{u_{t 2}^{2}} = \frac{4}{9} (\frac{L^{2}}{T^{2}}) \end{matrix}

(4676)

where:

$T$ is the turbulence time scale, $T = k / ε$ .
$L$ is the turbulence length scale, $L = k^{3 / 2} / ε$ .

$k$ is the turbulent kinetic energy and $ε$ is the dissipation rate.

In Simcenter STAR-CCM+ the total acoustic power per unit volume can be reported in dimensional units ( ${W/ m}^{3}$ ) and in dB:

Figure 19. EQUATION_DISPLAY

G_{A P} (dB) = 10 log (\frac{G_{A P}}{P_{r e f}})

(4677)

where $P_{r e f}$ is the reference acoustic power.

Proudman Noise Source Model

Like the Goldstein model, the Proudman noise source model evaluates acoustic power per unit volume, and the sound is from quadrupoles, such as the areas around blower blades. This model has been used for air handling subsystem (AHS) applications, including rotating parts (such as blowers), heat exchangers, and distribution ducts. The Proudman model assumes isotropic turbulence.

Proudman considers the generation of noise by isotropic turbulence. In Proudman’s high-Reynolds model for isotropic turbulence in near incompressible flow, the AP (acoustic power) per unit volume is:

Figure 20. EQUATION_DISPLAY

A P = α ρ_{0} \frac{u^{3}}{l} \frac{u^{5}}{c_{0}^{5}}

(4678)

where:

$α$ is a constant related to the shape of the longitudinal velocity correlation.
$u$ is the root mean square of one of the velocity components.
$l$ is the longitudinal integral length scale of the velocity.
$ρ_{0}$ is the far-field density.
$c_{0}$ is the far-field sound speed.

Different researchers have found different values for $α$ , ranging from 0.629 to 13. Simcenter STAR-CCM+ uses a re-scaled constant $α_{c}$ from Sarkar and Hussaini [912].

In Proudman’s paper [909], the characteristic velocity of energy-containing eddies $u$ can be written as:

Figure 21. EQUATION_DISPLAY

u = \sqrt{\frac{2}{3} k}

(4679)

In terms of the turbulence velocity scale and of the turbulence length scale, the local acoustic power due to the unit volume of isotropic turbulence (in ${W/ m}^{3}$ ) becomes:

Figure 22. EQUATION_DISPLAY

A P = α_{c} ρ_{0} \frac{U^{3}}{L} \frac{U^{5}}{a_{0}^{5}}

(4680)

with:

Figure 23. EQUATION_DISPLAY

U = \frac{L}{T}, α_{c} = 0.629

(4681)

where:

$ρ_{0}$ is the far-field density.
$U$ is the turbulence velocity.
$L$ is the turbulence length scale.
$T$ is the turbulence time scale.
$c$ is the far-field sound speed.

The rescaled constant $α_{c}$ is based on Direct Numerical Simulation for isotropic turbulence done by Sarkar and Hussaini [912].

The total acoustic power per unit volume can be reported in dimensional units ( ${W/ m}^{3}$ ) and in dB:

Figure 24. EQUATION_DISPLAY

A P (dB) = 10 log (\frac{A P}{P_{r e f}})

(4682)

where $P_{r e f}$ is the reference acoustic power.

Lilley Noise Source Model

The Lilley noise source models calculate the turbulent shear flow noise of quadrupole sources from the fluctuating velocity flow field.

Applications include problems where local shear effects dominate, such as flow around solid bodies and shear flows in channels. This model evaluates the location and strength of aeroacoustic sound sources. This model is available only for steady-state simulations.

The Lilley Noise Source model is compatible with the coupled and segregated flow models. Computational costs (specifically CPU time) depend on input of Number of Realizations and Number of Fourier Modes provided to the Stochastic Noise Generation and Radiation (SNGR) Model. The Lilley Noise Source model calculates three terms: Lilley Self-Noise Source, Lilley Shear-Noise Source, and Lilley Total-Noise Source.

The Lilley source terms are available for steady-state solutions computed using a Reynolds-Averaged Navier-Stokes (RANS) Turbulence model. A RANS model is the only type that can provide turbulence length scale and turbulent time scale that are dominated by local shear effects, as is the case of flow around solid bodies and shear flows in channels.

The Lilley equation can be written as:

Figure 25. EQUATION_DISPLAY

\frac{D}{D t} [\frac{D^{2} Π}{D t^{2}} - \frac{\partial}{\partial x_{j}} (c^{2} \frac{\partial Π}{\partial x_{j}})] + 2 [\frac{\partial u_{k}}{\partial x_{j}} \frac{\partial}{\partial x_{k}} (c^{2} \frac{\partial Π}{\partial x_{j}})] = - 2 [\frac{\partial u_{k}}{\partial x_{i}} \frac{\partial u_{j}}{\partial x_{k}} \frac{\partial u_{i}}{\partial x_{j}}] + ψ

(4683)

Figure 26. EQUATION_DISPLAY

ψ = 2 [\frac{\partial u_{j}}{\partial x_{i}} \frac{\partial}{\partial x_{j}} \frac{1}{ρ} \frac{\partial τ_{i k}}{\partial x_{k}}] - [\frac{D}{D t} \frac{\partial}{\partial x_{i}} \frac{1}{ρ} \frac{\partial τ_{i j}}{\partial x_{j}}] + [\frac{D^{2}}{D t^{2}} \frac{1}{c_{p}} \frac{D S}{D t}]

(4684)

where $c$ is the speed of sound, $τ_{i k}$ is the stress tensor and $ψ$ represents the effects of entropy fluctuations and fluid viscosity.

The entropy fluctuation is negligible for problems without heat transfer or combustion. Viscous effects are also negligible for a high Reynolds number flow. It is therefore usual to neglect these terms from the right-hand side. Then Eqn. (4683) becomes:

Figure 27. EQUATION_DISPLAY

\frac{D}{D t} [\frac{D^{2} Π}{D t^{2}} - \frac{\partial}{\partial x_{j}} (c^{2} \frac{\partial Π}{\partial x_{j}})] + 2 [\frac{\partial u_{k}}{\partial x_{j}} \frac{\partial}{\partial x_{k}} (c^{2} \frac{\partial Π}{\partial x_{j}})] = - 2 [\frac{\partial u_{k}}{\partial x_{i}} \frac{\partial u_{j}}{\partial x_{k}} \frac{\partial u_{i}}{\partial x_{j}}]

(4685)

where:

Figure 28. EQUATION_DISPLAY

Π = (\frac{c_{v}}{c_{p}}) ln \frac{p}{p_{0}}

(4686)

and $p_{0}$ is reference pressure.

By assuming that the flow satisfies the small perturbation assumption, the flow is locally linearized as follows:

Figure 29. EQUATION_DISPLAY

u_{i} (x, t) = U_{i} (x) + u_{i}' (x, t)

(4687)

where $U_{i} (x)$ is the mean velocity field and $u_{i}' (x, t)$ is the turbulent velocity field. The right-hand side of Eqn. (4685) can be expanded as follows:

Figure 30. EQUATION_DISPLAY

\begin{matrix} - 2 [\frac{\partial u_{k}}{\partial x_{i}} \frac{\partial u_{j}}{\partial x_{k}} \frac{\partial u_{i}}{\partial x_{j}}] = - 2 [\frac{\partial U_{k}}{\partial x_{i}} \frac{\partial U_{j}}{\partial x_{k}} \frac{\partial U_{i}}{\partial x_{j}}] - 2 [\frac{\partial u_{k}'}{\partial x_{i}} \frac{\partial u_{j}'}{\partial x_{k}} \frac{\partial u_{i}'}{\partial x_{j}}] - \\ 6 [\frac{\partial U_{k}}{\partial x_{i}} \frac{\partial U_{j}}{\partial x_{k}} \frac{\partial u_{i}'}{\partial x_{j}}] - 6 [\frac{\partial u_{k}'}{\partial x_{i}} \frac{\partial u_{j}'}{\partial x_{k}} \frac{\partial U_{i}}{\partial x_{j}}] \end{matrix}

(4688)

Figure 31. EQUATION_DISPLAY

A = - 2 [\frac{\partial U_{k}}{\partial x_{i}} \frac{\partial U_{j}}{\partial x_{k}} \frac{\partial U_{i}}{\partial x_{j}}]

(4689)

Figure 32. EQUATION_DISPLAY

B = S_{SelfNoiseTerm} = - 2 [\frac{\partial u_{k}'}{\partial x_{i}} \frac{\partial u_{j}'}{\partial x_{k}} \frac{\partial u_{i}'}{\partial x_{j}}]

(4690)

Figure 33. EQUATION_DISPLAY

C = S_{ShearNoiseTerm} = - 6 [\frac{\partial U_{k}}{\partial x_{i}} \frac{\partial U_{j}}{\partial x_{k}} \frac{\partial u_{i}'}{\partial x_{j}}] - 6 [\frac{\partial u_{k}'}{\partial x_{i}} \frac{\partial u_{j}'}{\partial x_{k}} \frac{\partial U_{i}}{\partial x_{j}}]

(4691)

where $A$ represents the mean flow shape change, the Self-Noise Term $B$ contains effects of the turbulent (fluctuating) velocity components, and the Shear Noise Term $C$ contains the interaction between the mean shear flow and turbulent velocity components.

The noise source terms of Lilley’s equation are evaluated based on mean velocity fields that are provided by a steady-state RANS solution and turbulent velocity components. These components are generated by the synthetic turbulence method of Bailly and Juve [877], Bechara et al. [878], and Kraichnan [900].

Linearized Euler Equation (LEE) Noise Source Model

The Linearized Euler Equations (LEE) account for refraction and convection effects in any sheared mean flows. The equations can be used for a wider range of conditions than the Lilley equation, where the associated source term is a nonlinear function of the fluctuating velocity flow field. See [878].

Note	This model is used for noise sources only, not for solving acoustic wave propagation.

This model is available only for steady-state simulations. As Lilley equation, the LEE Noise Source model computes LEE Self-Noise Source, LEE Shear Noise Source, and LEE Total Noise Source.

The linearized form of the Euler equations [878] derives from the nonlinear Euler equations. The linearized forms can be achieved by superimposing small perturbations of turbulent and acoustic components on the mean flow as follows:

Figure 34. EQUATION_DISPLAY

\begin{matrix} \begin{matrix} p_{i} (x, t) = P_{i} (x) + p_{i}' (x, t) + p_{a i} (x, t) \\ u_{i} (x, t) = U_{i} (x) + u_{i}' (x, t) + u_{a i} (x, t) \end{matrix} \\ ρ_{i} (x, t) = \overline{ρ_{i}} (x) + ρ_{i}' (x, t) + ρ_{a i} (x, t) \end{matrix}

(4692)

where the acoustic components $p_{a i}$ , $u_{a i}$ , $ρ_{a i}$ are small compared to the mean components $P_{i}$ , $U_{i}$ , $\overline{ρ_{i}}$ and the turbulent components $p_{i}'$ , $u_{i}'$ , $ρ_{i}'$ .

Including the decomposition of variables in Eqn. (4692), and considering the assumption that the acoustic perturbations are isentropic:

Figure 35. EQUATION_DISPLAY

p_{a} = c_{0}^{2} ρ_{a}

(4693)

and that turbulent density fluctuations ( $ρ′$ ) can be neglected, then the Linearized Euler equations for velocity components become:

Figure 36. EQUATION_DISPLAY

\begin{matrix} S = \frac{\partial u_{a i}}{\partial t} + U_{j} \frac{\partial u_{a i}}{\partial x_{j}} + u_{a j} \frac{\partial U_{i}}{\partial x_{j}} + \frac{1}{\bar{ρ}} \frac{\partial p_{a}}{\partial x_{i}} - \frac{ρ_{a}}{{\bar{ρ}}^{2}} \frac{\partial P}{\partial x_{i}} \\ = - U_{j} \frac{\partial {u^{'}}_{i}}{\partial x_{j}} - {u^{'}}_{j} \frac{\partial U_{i}}{\partial x_{j}} - {u^{'}}_{j} \frac{\partial {u^{'}}_{i}}{\partial x_{j}} - \frac{1}{\bar{ρ}} \frac{\partial p'}{\partial x_{i}} - \frac{\partial {u^{'}}_{i}}{\partial t} + \frac{\partial}{\partial x_{j}} (\bar{{u_{j}}^{'} {u_{i}}^{'}}) \end{matrix}

(4694)

The second set of terms includes the source terms responsible for sound generation.

The decomposition of the main sources of aerodynamically generated sound can be done onto the shear noise term $S_{ShearNoiseTerm}$ (representing the interaction between the mean shear velocities and turbulent velocity components of the flow) and the self-noise term $S_{SelfNoiseTerm}$ (representing turbulence-turbulence interactions):

Figure 37. EQUATION_DISPLAY

S_{ShearNoiseTerm} = {- U}_{j} \frac{\partial u_{i}'}{\partial x_{j}} - u_{j}' \frac{\partial U_{i}}{\partial x_{j}}

(4695)

Figure 38. EQUATION_DISPLAY

S_{SelfNoiseTerm} = - u_{j}' \frac{\partial u_{i}'}{\partial x_{j}}

(4696)

The turbulent velocity components are synthesized by the Stochastic Noise Generation and Radiation model.

The source terms in the Linearized Euler Equations, similar to source terms in the Lilley Equation, are available for steady-state solutions computed using a Reynolds-Averaged Navier-Stokes (RANS) Turbulence model that can provide turbulence length scale and turbulence time scale.

Stochastic Noise Generation and Radiation (SNGR) Model

The scope of the SNGR model is to compute a synthetic turbulence field.

A time-space turbulent velocity field is generated using random Fourier modes. This method, called the Stochastic Noise Generation and Radiation (SNGR) model, was proposed by Kraichnan [900] and Karweit et al. [898], and afterward developed by Bailly and Juve [877], Bechara et al. [878]. In Simcenter STAR-CCM+, the SNGR method requires user input of two properties of the Lilley noise source model: Number of Realizations and Number of Fourier Modes. See Lilley and LEE Noise Source Properties.

Consider a three-dimensional Fourier decomposition of a turbulent homogeneous isotropic field at a given point at location $x$ :

Figure 39. EQUATION_DISPLAY

u_{t} (x) = \int_{}^{} u_{t} (k) e^{(j k y)} d k

(4697)

where $u_{t}$ is the turbulent velocity field, $k$ is the wave vector, and $j$ is the imaginary unit, with $j^{2} = - 1$ .

This Fourier integral can be transformed into a limited sum of $n$ Fourier modes:

Figure 40. EQUATION_DISPLAY

u_{t} (x) = 2 \sum_{n = 1}^{N} u_{n} \cos (k_{n} \cdot x + ψ_{n}) σ_{n}

(4698)

where $u_{n}$ , $ψ_{n}$ and $σ_{n}$ are the amplitude, phase, and directional unit vector respectively of the $n$ -th Fourier mode associated with the wave vector $k_{n}$ .

The amplitude $u_{n}$ of each mode is computed so that the turbulence kinetic energy $E (k_{n})$ corresponds to the von Karman-Pao energy spectrum for isotropic, homogeneous turbulence:

Figure 41. EQUATION_DISPLAY

u_{n} = \sqrt{E (k_{n}) (Δ k_{n})}

(4699)

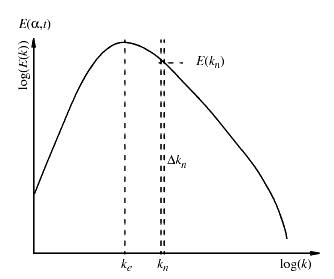
where $u_{n}$ is the amplitude of the mode and $Δ k_{n}$ is the small interval in the spectrum at $k_{n}$ .

The expression for the von Karman-Pao energy spectrum can be written as:

Figure 42. EQUATION_DISPLAY

E (k_{n}) = \frac{{S N G R}_{α} \overline{u^{2}}}{k_{e}} {(\frac{k}{k_{e}})}^{4} \frac{1}{{[{1 + (\frac{k}{k_{e}})}^{2}]}^{17 / 6}} e^{({- 2 (\frac{k}{k_{η}})}^{2})}

(4700)

where:

$k$ is the wavenumber.
$k_{η}$ is the Kolmogorov wavenumber.
$\overline{u^{2}}$ is the root-mean-square value of the velocity fluctuations corresponding to the turbulent kinetic energy.
${S N G R}_{α}$ is a numerical constant.
$k_{e}$ is the wavenumber corresponding to the most energy containing eddies at the peak in the spectrum.

Lighthill Equation

Lighthill's equation is an inhomogeneous wave equation that derives the acoustic field by analogy with the Navier-Stokes equations for a compressible fluid (Lighthill analogy [901]). In Lighthill's equation, the acoustic field is described by a second-order tensor known as the Lighthill turbulence stress tensor.

In component form, the mass and momentum conservation equations for a fluid read:

Figure 43. EQUATION_DISPLAY

\frac{\partial ρ}{\partial t} + \frac{\partial}{\partial x_{i}} (ρ ν_{i}) = 0

(4701)

Figure 44. EQUATION_DISPLAY

\frac{\partial}{\partial t} (ρ ν_{i}) + \frac{\partial}{\partial x_{j}} (ρ ν_{i} ν_{j} + p_{i j}) = 0

(4702)

where:

$ρ$ is density.
$ν_{i}$ and $ν_{j}$ are the velocity components.
$p_{i j}$ is the stress tensor.
Figure 45. EQUATION_DISPLAY

$p_{i j} = {- σ}_{i j} + (p - p_{0}) δ_{i j}$
(4703)

where

$p$ is the thermodynamic pressure of the flow field, that is, the working pressure.
$δ_{i j}$ is the Kronecker delta.
$σ_{i j}$ is the viscous stress tensor.
Figure 46. EQUATION_DISPLAY

$σ_{i j} = μ (\frac{\partial ν_{i}}{\partial x_{j}} + \frac{\partial ν_{j}}{\partial x_{i}} - \frac{2}{3} \frac{\partial ν_{i}}{\partial x_{i}} δ_{i j})$
(4704)

Using Einstein notation, Lighthill’s equation can be written as:

Figure 47. EQUATION_DISPLAY

\frac{\partial^{2} ρ}{\partial t^{2}} - c_{0}^{2} (\nabla^{2} ρ) = \frac{\partial^{2} T_{i j}}{(\partial x_{i}) (\partial x_{j})}

(4705)

where $T_{i j}$ is the “Lighthill turbulence stress tensor” for the acoustic field.

Figure 48. EQUATION_DISPLAY

T_{i j} = ρ ν_{i} ν_{j} + p_{i j} - c_{0}^{2} (ρ - ρ_{0}) δ_{i j}

(4706)

substitute Eqn. (4704) into Eqn. (4706) to get:

Figure 49. EQUATION_DISPLAY

T_{i j} = ρ ν_{i} ν_{j} - σ_{i j} + δ_{i j} [(p - p_{0}) - {c_{0}}^{2} (ρ - ρ_{0})]

(4707)

where $ρ_{0}$ is the far field density.

In laminar flow, the viscous stress tensor is given by:

Figure 50. EQUATION_DISPLAY

σ_{i j} = σ_{i j, lam} = μ (\frac{\partial ν_{i}}{\partial x_{j}} + \frac{\partial ν_{j}}{\partial x_{i}} - \frac{2}{3} \frac{\partial ν_{i}}{\partial x_{i}} δ_{i j})

(4708)

In turbulent flow, the viscous stress tensor is given by:

Figure 51. EQUATION_DISPLAY

σ_{i j} = σ_{i j, lam} + σ_{i j, turb} = μ_{e f f} (\frac{\partial ν_{i}}{\partial x_{j}} + \frac{\partial ν_{j}}{\partial x_{i}} - \frac{2}{3} \frac{\partial ν_{i}}{\partial x_{i}} δ_{i j})

(4709)

where the effective viscosity is $μ_{e f f} = μ + μ_{t}$ , the sum of the laminar and turbulent viscosities.

In inviscid flow, the viscous stress tensor is $σ_{i j} = 0$ .

Each of the source terms in Eqn. (4707) describes a significant role in the generation of sound as:

$ρ ν_{i} ν_{j}$ describes unsteady convection of flow (or Reynold’s Stress)
$σ_{i j}$ describes sound shear
$δ_{i j} (p - c_{0}^{2} ρ)$ describes nonlinear acoustic generation processes

Mesh Frequency Cutoff Formulation

The main value in performing a mesh-frequency cutoff analysis of a steady-state solution is to determine in advance of a transient calculation whether the chosen grid has sufficient resolution to capture the turbulence flow structures in the frequency range of interest.

Mendonça [907] shows that, given a cell dimension $D$ and local turbulent kinetic energy $k$ , the smallest length scale of a turbulent eddy structure that is captured by the mesh is $2 D$ ; its associated isotropic fluctuation velocity is $\sqrt{(2 / 3) k}$ . Therefore the maximum frequency $f_{M C}$ reasonably resolved by the local grid spacing $D$ is:

Figure 52. EQUATION_DISPLAY

f_{M C} = \frac{\sqrt{\frac{2}{3} k}}{2 Δ}

(4710)

$k$ represents the mean turbulent kinetic energy that is contained by the mean turbulent structures. Most widely used RANS turbulence models solve transport equations for $k$ directly. The transport-equation for $k$ is derived directly from the unsteady Navier-Stokes equations, and therefore it contains contributions from all the important mechanisms: convection, diffusion, production, and dissipation. So long as the mean flow features are captured, the $k$ solution tends to be reasonably grid-independent.

This measure is used in preference to one derived from the turbulence time scale, that is, the ratio of kinetic energy to its dissipation rate $k / ϵ$ . This is better representative of the dissipative scales which, in frequency and energy content, are orders of magnitude higher than the human hearing range or peak sensitivity.

Since this measure is derived from a steady-state solution, some limitations are inherent. The frequencies that are associated with time varying large-scale motions such as vortex-shedding, which convect through the mesh, are not accounted for. Instead, its usefulness is to approximate the frequencies of the turbulence scales which are modeled in RANS, and which become resolved in Large Eddy Simulation. In other words, this measure is more valid for the broadband and less so for narrowband excitations.

The mesh frequency cutoff measure has been applied to typical industrial applications at low Mach numbers flow.