Home
Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
Compressible Flow
The tutorials in this set illustrate various Simcenter STAR-CCM+ features for compressible fluid flows as well as harmonic balance.
Gas Turbine Aerodynamics: Post-Processing
In turbomachinery studies, the analysis of the flow field throughout the blade passage requires advanced post processing methods.
Projecting Isosurface Data to an Embedded Plane
In a highly-curved blade passage some areas of an isosurface can be obscured from view. To overcome this problem, you can project the isosurface onto a 2D plane located within the blade passage.

Share

Link: copied

Breadcrumb: copied

Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
- Using Tutorial Macros and Files
  Macros, input files, and final simulation files for a range of tutorials are provided as an optional download package on the Support Center website. These macros and final simulation files are provided as an aid to the written tutorials, so that you can check your final results against the downloaded files, or against a simulation that is built and run using the macros.
- Introduction
  Welcome to the Simcenter STAR-CCM+ introductory tutorial. In this tutorial, you explore the important concepts and workflow. Complete this tutorial before attempting any others.
- Foundation Tutorials
  The foundation tutorials showcase the major features of Simcenter STAR-CCM+ in a series of short tutorials.
- Geometry
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for creating and working with parts and 3D-CAD.
- Mesh
  The tutorials in this set illustrate various STAR-CCM+ features for building CFD meshes.
- Incompressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for incompressible fluid flows as well as porosity and solution recording
- Compressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for compressible fluid flows as well as harmonic balance.
  - Subsonic Flow: NACA-Type Intake
    This tutorial illustrates how to solve a three-dimensional compressible flow problem using Simcenter STAR-CCM+.
  - Transonic Flow: RAE2822 Airfoil
    The tutorial simulates two-dimensional, turbulent, compressible, transonic air flow over an idealized airfoil.
  - Transonic Flow: RAE2822 Airfoil Using Overset Mesh
    This tutorial demonstrates how to use an overset mesh to simulate transonic flow over the RAE2822 airfoil.
  - Anisotropic Volume Meshing: Onera M6 Wing
    When meshing aerospace geometries such as wings, propeller blades, or turbine blades, you are required to generate a very fine mesh that adequately captures the curvature of the leading and trailing edges. To help reduce the cell count while maintaining solution accuracy, Simcenter STAR-CCM+ provides an anisotropic meshing option by which you can refine these edges.
  - Adaptive Mesh Refinement: Hypersonic Flow
    Hypersonic flows and flight envelopes present unique challenges in Computational Flow Dynamics. The extreme gradients and shocks can push flow solvers to their limits and resolving the flow features, particularly shock formation, is of paramount importance in obtaining valid converged solutions. In Simcenter STAR-CCM+, you can apply Adaptive Mesh Refinement (AMR) to accurately resolve developing shocks using refinement based on solution gradients.
  - Harmonic Balance: Single Stage Periodic Flow
    The tutorial illustrates the steps necessary to simulate a single axial compressor blade row so that the effect of a periodic wake can be analyzed using the Harmonic Balance method.
  - Gas Turbine Aerodynamics: Post-Processing
    In turbomachinery studies, the analysis of the flow field throughout the blade passage requires advanced post processing methods.
    - Loading the Initial Simulation
      As this tutorial focuses on post-processing of gas turbine aerodynamic cases, the start file contains a fully defined simulation modeling the steady turbulent flow of an ideal gas through a simplified turbine stage.
    - Generating the Solution
      For this tutorial the starting simulation file contains the complete mesh operation pipeline by which you generate a volume mesh. After generating the mesh, you can run the simulation and verify the result.
    - Parameterizing the Flowpath
      Simcenter STAR-CCM+ provides a parameterization object in which you can define the coordinate system and surfaces by which the domain is normalized.
    - Viewing the Solution on a Blade-to-Blade Isosurface
      A spanwise isosurface provides a surface of revolution at a specified spanwise position. Rendering solution data on this type of isosurface gives you an accurate picture of the flow behaviour across the blade rows in the passage.
    - Projecting Isosurface Data to an Embedded Plane
      In a highly-curved blade passage some areas of an isosurface can be obscured from view. To overcome this problem, you can project the isosurface onto a 2D plane located within the blade passage.
    - Plotting the Blade Load
      Assessing blade load is a core study in turbomachinery design. By applying the blade parameterization, you can create a plot in which the pressure profile is unwrapped along the chosen section.
    - Creating a 2D Surface Averaged View
      Simcenter STAR-CCM+ allows you to reduce the full 3D solution within the blade passage to a single 2D surface-averaged plot with optional data weighting.
    - Creating a Profile Average Plot
      For any surface of revolution you can view the average solution of any scalar value along this surface.
- Heat Transfer and Radiation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for heat transfer, radiation, and thermal comfort.
- Multiphase Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating multiphase fluid flow problems
- Discrete Element Method
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating Discrete Element Method problems
- Motion
  The tutorials in this set illustrate various STAR-CCM+ features for simulating problems with moving geometries and meshes, dynamic fluid body interaction, and rigid body motion:
- Reacting Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating reacting flows such as combustion.
- Solid Stress
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for computing deformation, strain, and stresses in solid regions. They also show how such computations can be coupled to the fluid behavior in an analysis of fluid-structure interaction.
- Aeroacoustics
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for solving aeroacoustic simulations.
- Electromagnetism
  The following tutorials illustrate features for solving problems that involve electromagnetic fields.
- Electrochemistry
  The following tutorial demonstrates chemical reactions induced by an electrical current.
- Battery
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for setting up a battery model:
- Automation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ automation and macro features.
- Design Exploration
  The tutorials in this set illustrate various features for running design exploration studies in Design Manager.
- Coupling with CAE Codes
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for coupling with CAE codes:
- Analysis Methods
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for analysing and visualizing simulation data.
- Simcenter STAR-CCM+ In-cylinder
  The tutorials in this set illustrate features for simulating internal combustion engines in Simcenter STAR-CCM+ using the dedicated add-on Simcenter STAR-CCM+ In-cylinder.

Projecting Isosurface Data to an Embedded Plane

In a highly-curved blade passage some areas of an isosurface can be obscured from view. To overcome this problem, you can project the isosurface onto a 2D plane located within the blade passage.

To achieve a flattened projection of the isosurface, you must assign the conformal embedding transform of the parameterization to the transform property of the relevant displayer.

To apply the embedding transform:

To make a copy of the Scalar: Blade to Blade scene, select the Scenes > Scalar: Blade to Blade node and drag onto the Scenes node.
Rename the copy to Scalar: Blade to Blade Projected.
Right-click the Scenes > Scalar: Blade to Blade Projected > Outline 1 node and select Delete.
Select the Scalar 1 node and set Transform to Embedding: Axisymmetric 1 (Conformal).
The conformal embedding transform uses the $m' θ$ transform scheme. This transform scheme means that the $m'$ values (which were calculated during the parameterization) are mapped to the x coordinate and the $θ$ values are mapped to the y coordinate. This mapping ensures that the angles are conserved while the lengths are distorted.
To view the projected results, in the Vis toolbar, click (Save-Restore-Select Views) and select Views > -Z > Up -Y
The scene is as shown below:

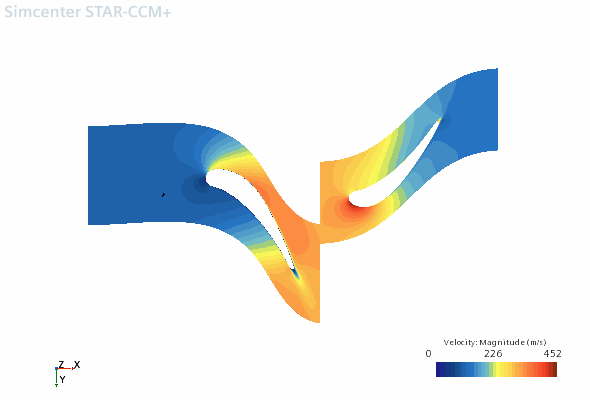
As well as visualizing the data as a scalar scene, you can also view data on an embedded vector scene:

Right-click Scalar: Blade to Blade Projected and select New Displayer > Vector.
Expand the Scenes > Scalar: Blade to Blade Projected > Vector 1 node and set the following properties:
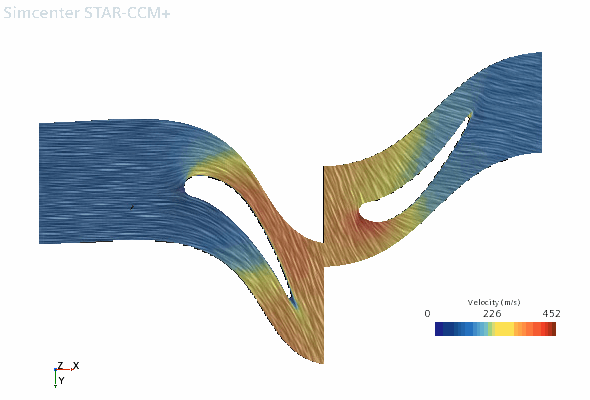
Node Property Setting
Vector 1 Display Mode Line Integral Convolution
Transform Embedding: Axisymmetric 1 (Conformal)
Parts Parts Derived Parts > Isosurface
Vector Field Function Velocity > Lab Frame Reference
Right-click the Scalar: Blade to Blade Projected > Scalar 1 node and select Toggle Visibility.
To view the projected results, in the Vis toolbar, click (Save-Restore-Select Views) and select Views > -Z > Up -Y.
The scene is shown below: