Stress

Stress is a measure of the force per unit area acting on a surface. In a solid structure, external forces or temperature changes induce a stress field, which can lead to motion and deformation of the solid structure. Internal forces that oppose the deformation of the structure also induce an internal elastic stress that tends to restore the structure to the original undeformed state. Some materials also present built-in stress, that exists in absence of applied forces and deformations.

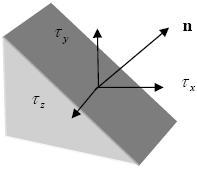
In general, the stress acting on a plane section of a body is defined by a vector $τ$ , which is known as stress vector, or traction, as:

Figure 1. EQUATION_DISPLAY

τ = (\begin{matrix} τ_{x} \\ τ_{y} \\ τ_{z} \end{matrix}) = (\begin{matrix} F_{x} / A \\ F_{y} / A \\ F_{z} / A \end{matrix})

(4432)

where $F$ is the force acting on the plane and $A$ is the area of the plane.

The stress at a point is the force per unit area, as the area over which the force is applied approaches zero. At a point, there is an infinite number of plane sections of the body. However, the state of stress at the point is completely defined by the stress vectors that are associated with three mutually perpendicular planes passing through the point. Therefore, the state of stress at any point, on any plane, is defined by a second-order tensor of the following form:

Figure 2. EQUATION_DISPLAY

σ = (\begin{matrix} {\begin{matrix} σ \end{matrix}}_{x x} & {\begin{matrix} σ \end{matrix}}_{x y} & {\begin{matrix} σ \end{matrix}}_{x z} \\ {\begin{matrix} σ \end{matrix}}_{y x} & {\begin{matrix} σ \end{matrix}}_{y y} & {\begin{matrix} σ \end{matrix}}_{y z} \\ {\begin{matrix} σ \end{matrix}}_{z x} & {\begin{matrix} σ \end{matrix}}_{z y} & {\begin{matrix} σ \end{matrix}}_{z z} \end{matrix})

(4433)

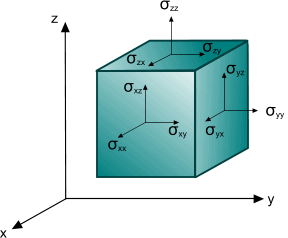
Since the sum of moments must go to zero as the body volume shrinks to zero, the stress tensor is symmetric.

The off-diagonal terms are called shear stresses, since they act tangentially to a face. The diagonal terms are referred to as normal stresses, since they act normal to a face.

The stress vector on a plane can be written as the matrix product:

Figure 3. EQUATION_DISPLAY

τ = σ \cdot n = (\begin{matrix} σ_{x x} & σ_{x y} & σ_{x z} \\ σ_{y x} & σ_{y y} & σ_{y z} \\ σ_{z x} & σ_{z y} & σ_{z z} \end{matrix}) (\begin{matrix} n_{x} \\ n_{y} \\ n_{z} \end{matrix})

(4434)

where

n

is the unit vector normal to the plane.

Simple states of stress include:

Volumetric Stress—The stress across a material is the same in all directions.
Plane Stress—Thin materials with no loading on the planar surfaces are in a state of plane stress, that is, the stress in the direction normal to the planar surfaces is zero (for example, if the planar surfaces lie on the x-y plane, the stress in the z-direction is zero, $σ_{z z} = σ_{x z} = σ_{y z} = 0$ ).
Uniaxial Stress—All but one of the stress components are zero, for example $σ_{x x} \neq 0, σ_{y y} = σ_{z z} = σ_{x y} = σ_{y z} = σ_{z x} = 0$ .
Biaxial Stress—All but two axial components are zero, for example $σ_{x x} \neq 0 σ_{y y} \neq 0, σ_{z z} = σ_{x y} = σ_{y z} = σ_{z x} = 0$ .
Shear Stress—All but the stress components along the x, y and z axes are non-zero.

Stress Definitions

Stress can be defined in various ways. For example, you can define it in either the undeformed configuration or in the deformed configuration. For infinitesimal strains (see Eqn. (4444)), the undeformed and deformed configurations are equivalent.

Cauchy Stress: The stress tensor in Eqn. (4433) is defined in the deformed configuration and is more formally called Cauchy stress, or true stress. Cauchy stress is a direct measure of the traction acting on any surface of the body, in the current configuration. For output, Simcenter STAR-CCM+ uses the Cauchy stress.
Second Piola-Kirchhoff Stress: The second Piola-Kirchhoff stress tensor $S$ is defined as:; Figure 4. EQUATION_DISPLAY

$S = \det (F) F^{- 1} σ F^{- T}$
(4435); where $σ$ is the Cauchy stress and $F$ is the deformation gradient tensor in Eqn. (4428).
Principal Stresses: At any point in the solid, there are always three planes, called principal planes, on which the shear stress (that is, the tangential component of the stress vector) is zero. The stress vectors associated with these planes are given by:
Figure 5. EQUATION_DISPLAY

$s_{k} = s_{k} n_{k}$
(4436)

where $n_{k}$ with $i = 1, 2, 3$ denotes the principal plane normals and $s_{k}$ denotes the eigenvalues of $σ$ (see Eqn. (5209)). The eigenvalues of $σ$ are called the principal stresses, where $s_{1}$ is the maximum principal stress, $s_{3}$ is the minimum principal stress, and $s_{2}$ is the intermediate principal stress, with $s_{1} \geq s_{2} \geq s_{3}$ .; If the material is in a hydrostatic state of stress, all principal stresses are equal.; Solid mechanics uses the convention where stresses are positive when in tension and negative in compression, so the maximum principal is the most tensile. For this reason, it is often used as a measure of tensile failure in a material.
Maximum Shear Stress: On one plane, the shear stress is a maximum. The maximum shear stress is an important measure of ductile failure associated with plastic behavior. It is defined as:
Figure 6. EQUATION_DISPLAY

$τ_{\max} = \frac{(s_{1} - s_{3})}{2}$

(4437)

with $s_{1}$ and $s_{2}$ given by Eqn. (4436).
Mean Stress: The mean stress, or pressure, is defined as:
Figure 7. EQUATION_DISPLAY

$σ_{m} = p = \frac{1}{3} t r (σ) = \frac{(s_{1} + s_{2} + s_{3})}{3}$

(4438); If the material is in a hydrostatic state of stress, the mean stress is interpreted as the negative of the pressure.
Deviatoric Stress: The deviatoric stress is useful for describing plastic yielding and ductile failure. It is defined as:
Figure 8. EQUATION_DISPLAY

$σ^{d} = σ - σ_{m} I$

(4439)
von Mises Stress: The von Mises stress is an important measure of ductile failure. It represents the magnitude of the deviatoric stress and is independent of the mean stress:
Figure 9. EQUATION_DISPLAY

$σ_{v m} = \sqrt{\frac{1}{2} ({(s_{1} - s_{2})}^{2} + {(s_{1} - s_{3})}^{2} + {(s_{2} - s_{3})}^{2})}$

(4440); If the material is in a state of uniaxial stress, the von Mises stress is equal to the nonzero component of the stress. Often, material yielding is studied by loading coupons which are approximately in a uniaxial state of stress.