Correlations for ReTheta_t

A well-established correlation for $R{e}_{\theta t}$ was developed by Abu-Ghannam and Shaw [374].

In the case of a zero pressure gradient, this correlation is:

where $Tu$ is the turbulence intensity.

An alternative expression, developed for the Gamma ReTheta transition model by Menter et al. [380] is:

and this was later revised by Langtry [378] with a view to improving the results at lower free-stream turbulence intensities, as follows:

The three zero-pressure gradient correlations are plotted in the following figure. All three are provided in Simcenter STAR-CCM+ to allow the user flexibility to customize the correlations, but Eqn. (1530) is the default correlation used in the internal “Suluksna-Juntasaro” calibration.

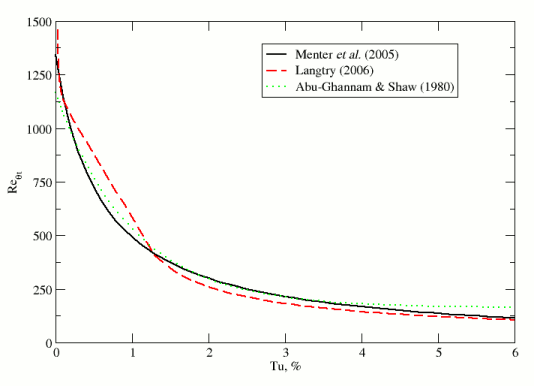
${\mathrm{Re}}_{\theta t}$ vs. Free-Stream Turbulence Intensity

The three correlations presented for zero pressure gradient in Eqn. (1528) through Eqn. (1530) were originally presented in a form that include the effects of a pressure gradient. There is some doubt that the pressure gradient effects are required in the ${\mathrm{Re}}_{\theta t}$ correlation [385], since they arguably introduce a double-accounting of the pressure gradient effects, but they are nevertheless optionally included in Simcenter STAR-CCM+. In the presence of a pressure gradient, the correlations require the computation of the Thwaites parameter, ${\lambda }_{\theta }$, and in the case of the Menter et al. [380] correlation, the acceleration parameter, $K$.

Thwaite’s parameter ${\lambda }_{\theta }$ is defined as:

where:

The parameter $K$ is defined as:

$s$ denotes the wall-parallel direction, where the local coordinate system is constructed using the flow direction and the wall-normal direction.

The turbulence intensity is obtained from the turbulent kinetic energy as follows:

The streamwise velocity gradient is calculated as:

where ${\overline{\mathbf{\text{v}}}}^T$ denotes the transpose of $\overline{v}$.

Since the momentum thickness $\theta$ must be derived from the momentum thickness Reynolds number ${\mathrm{Re}}_{\theta }$, the correlation becomes an implicit function that is solved iteratively.

The non-zero pressure gradient (NZPG) correlation of Abu-Ghannam and Shaw [374] is:

where:

For numerical robustness, the following limits are applied:

The NZPG correlation of Menter et al. [380] is:

where:

For numerical robustness, the following limits are applied:

The NZPG correlation of Langtry [378] is:

For numerical robustness, the following limits are applied:

A comparison of the three NZPG correlations is shown in the following figure for a range of free-stream turbulence intensities.

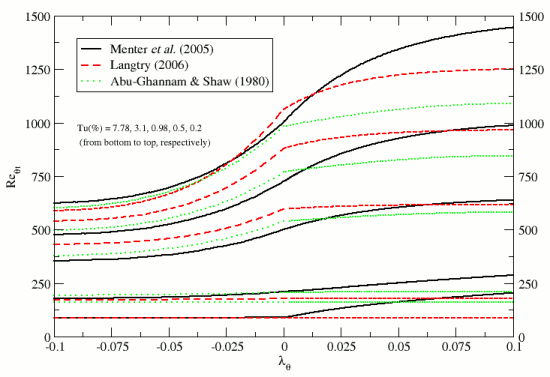
${\mathrm{Re}}_{\theta t}$ vs. ${\lambda }_{\theta }$ for various values of Free-Stream Turbulence Intensity