Fuel Saturation Distribution

Before fuel droplets evaporate and mix homogeneously throughout a cell, the evaporated fuel is initially located in close proximity to the fuel droplets. The Fuel Saturation Distribution model uses a fuel mass fraction profile to account for the initially uneven distribution of fuel mass fraction in a cell.

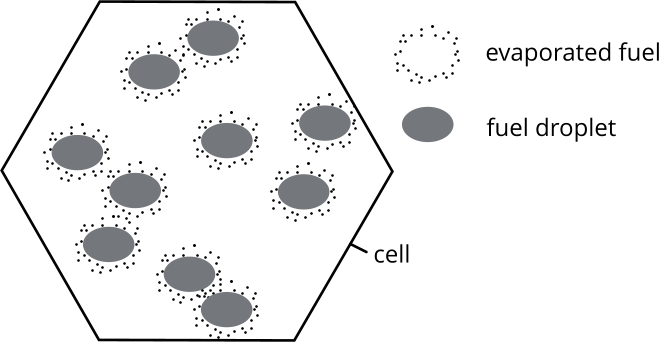
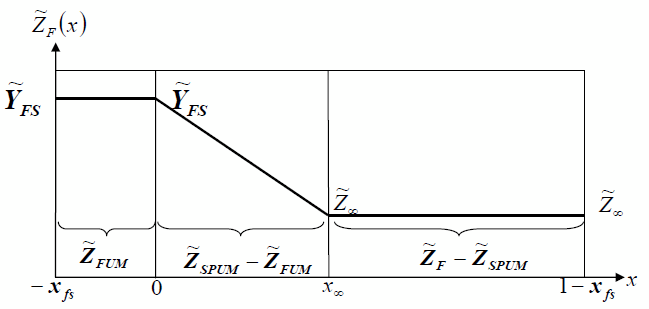
The Fuel Saturation Distribution model recognizes three zones related to the distance from fuel droplets.


Mass Fraction Profile Zone	Fuel Mass Fraction	Mass Fraction	Analytical Profile of ${\tilde{Z}}_{F} (x)$
1 Uniform zone with a fuel mass fraction corresponding to saturation conditions near the surface of the fuel droplets.	${\tilde{Z}}_{F U M}$	${\tilde{Z}}_{F} (0) = {\tilde{Y}}_{F S}$	$\begin{matrix} {\tilde{Z}}_{F} (x) = {\tilde{Y}}_{F S} & \forall x \in [- x_{f s}, 0] \end{matrix}$
2 A linear zone between the saturation conditions and the perfectly mixed zone.	${\tilde{Z}}_{S P U M} - {\tilde{Z}}_{F U M}$	${\tilde{Z}}_{F} (x_{\infty}) = {\tilde{Z}}_{\infty}$	$\begin{matrix} {\tilde{Z}}_{F} (x) = {\tilde{Y}}_{F S} + \frac{{\tilde{Z}}_{\infty} - {\tilde{Y}}_{F S}}{x_{\infty}} x & \forall x \in [0, x_{\infty}] \end{matrix}$
3 Uniform zone with a perfectly mixed fuel mass fraction.	${\tilde{Z}}_{F} - {\tilde{Z}}_{S P U M}$	${\tilde{Z}}_{\infty}$	$\begin{matrix} {\tilde{Z}}_{F} (x) = {\tilde{Z}}_{\infty} & \forall x \in [x_{\infty}, 1 - x_{f s}] \end{matrix}$

{\tilde{Z}}_{S P U M}

and

{\tilde{Z}}_{F U M}

are given by the following transport equations:

Figure 1. EQUATION_DISPLAY

\frac{\partial (\bar{ρ} {\tilde{Z}}_{S P U M})}{\partial t} + \nabla\cdot (\bar{ρ} {\tilde{v} \tilde{Z}}_{S P U M}) = \nabla\cdot (\bar{ρ} {D \nabla \tilde{Z}}_{S P U M}) + \tilde{S} - {\tilde{T}}_{S P U M}

(3949)

Figure 2. EQUATION_DISPLAY

\frac{\partial (\bar{ρ} {\tilde{Z}}_{F U M})}{\partial t} + \nabla\cdot (\bar{ρ} {\tilde{v} \tilde{Z}}_{F U M}) = \nabla\cdot (\bar{ρ} D {\tilde{Z}}_{F U M}) + \tilde{S} - {\tilde{T}}_{F U M}

(3950)

in which

\tilde{S}

is the droplet evaporation source term.

{\tilde{T}}_{S P U M}

and

{\tilde{T}}_{F U M}

are transfer terms from non-mixed non-homogenous zones to the completely mixed and homogenous profile zone 3.

{\tilde{T}}_{S P U M}

and

{\tilde{T}}_{F U M}

are assumed to be given by:


${\tilde{T}}_{S P U M}$	( ${\tilde{Y}}_{F S}$ defined)	Figure 3. EQUATION_DISPLAY ${\tilde{T}}_{S P U M} = \bar{ρ} K_{s p u m} [{\tilde{Y}}_{F S} - {\tilde{Z}}_{\infty}] \frac{C ({Re}_{t})}{τ} {\tilde{Z}}_{S P U M}$ (3951)
${\tilde{T}}_{S P U M}$	( ${\tilde{Y}}_{F S}$ not defined)	Figure 4. EQUATION_DISPLAY ${\tilde{T}}_{S P U M} = \bar{ρ} K_{s p u m} \frac{C ({Re}_{t})}{τ} {\tilde{Z}}_{S P U M}$ (3952)
${\tilde{T}}_{F U M}$	( ${\tilde{Y}}_{F S}$ defined)	Figure 5. EQUATION_DISPLAY ${\tilde{T}}_{F U M} = \bar{ρ} (K_{s p u m} + K_{f u m}) [{\tilde{Y}}_{F S} - {\tilde{Z}}_{\infty}] \frac{C ({Re}_{t})}{τ} {\tilde{Z}}_{F U M}$ (3953)
${\tilde{T}}_{F U M}$	( ${\tilde{Y}}_{F S}$ not defined)	Figure 6. EQUATION_DISPLAY ${\tilde{T}}_{F U M} = \bar{ρ} (K_{s p u m} + K_{f u m}) \frac{C ({Re}_{t})}{τ} {\tilde{Z}}_{F U M}$ (3954)

The fuel mass fraction at the surface of the droplets

{\tilde{Y}}_{F S}

in a given cell, assuming saturation conditions at the liquid-gas interface, is given by:

Figure 7. EQUATION_DISPLAY

{\tilde{Y}}_{F S} = \frac{P_{s a t} M_{W, F}}{M_{W, S} P}

(3955)

$P_{s a t}$ is the saturation vapor pressure (given by a saturation curve of the specified fuel as a function of the temperature of the fuel droplets).
$M_{W, F}$ is the molar weight of the fuel.
$P$ is the gas pressure within the cell.
$M_{W, S}$ is the molar weight of the gas mixture at the surface of the droplets within a cell.