Home
Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
Solid Stress
The tutorials in this set illustrate various Simcenter STAR-CCM+ features for computing deformation, strain, and stresses in solid regions. They also show how such computations can be coupled to the fluid behavior in an analysis of fluid-structure interaction.
Linear Stress Analysis: Cantilever I Beam
This tutorial demonstrates the basic concepts and workflow for linear FE (Finite Element) structural analyses in Simcenter STAR-CCM+.

Share

Link: copied

Breadcrumb: copied

Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
- Using Tutorial Macros and Files
  Macros, input files, and final simulation files for a range of tutorials are provided as an optional download package on the Support Center website. These macros and final simulation files are provided as an aid to the written tutorials, so that you can check your final results against the downloaded files, or against a simulation that is built and run using the macros.
- Introduction
  Welcome to the Simcenter STAR-CCM+ introductory tutorial. In this tutorial, you explore the important concepts and workflow. Complete this tutorial before attempting any others.
- Foundation Tutorials
  The foundation tutorials showcase the major features of Simcenter STAR-CCM+ in a series of short tutorials.
- Geometry
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for creating and working with parts and 3D-CAD.
- Mesh
  The tutorials in this set illustrate various STAR-CCM+ features for building CFD meshes.
- Incompressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for incompressible fluid flows as well as porosity and solution recording
- Compressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for compressible fluid flows as well as harmonic balance.
- Heat Transfer and Radiation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for heat transfer, radiation, and thermal comfort.
- Multiphase Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating multiphase fluid flow problems
- Discrete Element Method
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating Discrete Element Method problems
- Motion
  The tutorials in this set illustrate various STAR-CCM+ features for simulating problems with moving geometries and meshes, dynamic fluid body interaction, and rigid body motion:
- Reacting Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating reacting flows such as combustion.
- Solid Stress
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for computing deformation, strain, and stresses in solid regions. They also show how such computations can be coupled to the fluid behavior in an analysis of fluid-structure interaction.
  - Linear Stress Analysis: Cantilever I Beam
    This tutorial demonstrates the basic concepts and workflow for linear FE (Finite Element) structural analyses in Simcenter STAR-CCM+.
    - Prerequisites
      The instructions in the Linear Stress Analysis - Cantilever I Beam tutorial assume that you are already familiar with certain techniques in Simcenter STAR-CCM+.
    - Importing the Geometry
      Launch Simcenter STAR-CCM+ and import the 3D-CAD beam geometry that is provided for this tutorial.
    - Assigning the Imported Part to a Region
      Before you generate a mesh for the imported part, the part must be assigned to a Simcenter STAR-CCM+ region. As all the boundary conditions for this case are set directly on the part surfaces using segments, you can group all part surfaces under a single region boundary.
    - Selecting the Physics Models and Materials
      Select physics models to set up a static linear analysis and specify the beam material.
    - Applying Loads and Constraints Using Segments
      Using Simcenter STAR-CCM+ segments, apply a shear load to the free end of the beam and constrain the end at the wall to prevent motion.
    - Generating the Hexahedral Mesh
      In this tutorial, you mesh the beam with 3D solid hexahedral elements using the Simcenter STAR-CCM+ Directed Mesher.
    - Preparing Analysis Objects
      Set up scenes and reports to monitor the solution.
    - Running the Simulation
      Specify appropriate running settings for this simulation. As this is a linear problem, you are likely to obtain a good solution within the first iteration. For a linear problem, it is good practice to make sure that the residuals drop at least 6 orders of magnitude within the second iteration.
    - Visualizing the Solution
      Visualize the solution for the displacement and stress.
    - Summary
      This tutorial demonstrated the workflow for linear FE (Finite Element) structural analyses in Simcenter STAR-CCM+.
  - Plane Stress: Plate with Circular Hole in a Tensile Field
    This tutorial demonstrates how to set up a linear elastic FE (Finite Element) stress analysis in Simcenter STAR-CCM+.
  - Hyperelastic Stress Analysis with Adaptive Time-Step: Trileaflet Heart Valve
    Trileaflet valves are prosthetic heart valves that open and close because of the deformation of the flexible leaflets [reflink]. Obtaining a successful simulation of the valve opening event is challenging due to the snap through instability on which the valve operation depends. Simcenter STAR-CCM+ provides a dynamic time-step control that makes a successful simulation possible.
  - Normal Modes Solver: Wind Turbine Blade
    In solid mechanics, normal modes describe the oscillating motion of a solid body at a set of fixed frequencies, known as natural (or resonant) frequencies of the body.
  - Conjugate Heat Transfer and Thermal Stress: Exhaust Manifold
    Simcenter STAR-CCM+ allows you to combine the advantages of the finite volume (FV) and the finite element (FE) methods together in the same simulation.
  - Thermal Stress from Mapped Temperature Data: Exhaust Manifold
    This tutorial demonstrates how to perform thermal stress analysis in Simcenter STAR-CCM+.
  - Fluid-Structure Interaction: Vibrating Pipe
    This tutorial demonstrates how to set up fluid-structure interaction (FSI) problems in Simcenter STAR-CCM+.
  - FSI with Prescribed Solid Motion: Flapping Wing
    In Simcenter STAR-CCM+, you can analyse the two-way coupled fluid-structure interaction of systems whose motion paths are described by multiple superposed motions.
  - FSI and 6-DOF Motion: Stress Analysis on Boat Propeller
    In fluid-structure interaction simulations, you can define the motion of a solid structure relative to the motion of a 6-DOF body. A typical application is the analysis of the mechanical stresses on propellers attached to marine vessels.
  - FSI with Opening and Closing Flow Paths: Diaphragm Valve
    Simcenter STAR-CCM+ provides the capability of performing a two-way coupled fluid-structure interaction (FSI) simulation with opening and closing flow paths, which are due to the deformation of a hyperelastic non-linear material such as rubber. This capability can aid in the design of (but is not limited to) seals, valves, and gaskets used within a range of industries.
  - FSI Remeshing and Tessellated Geometry Parts Contact: Rubber Sleeve
    Simcenter STAR-CCM+ allows you to model the mechanical contact between a deformable structure and the tessellated surfaces of geometry parts within the simulation. This is useful to simulate the interaction between an elastic solid and a rigid obstacle, without modeling the obstacle explicitly.
- Aeroacoustics
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for solving aeroacoustic simulations.
- Electromagnetism
  The following tutorials illustrate features for solving problems that involve electromagnetic fields.
- Electrochemistry
  The following tutorial demonstrates chemical reactions induced by an electrical current.
- Battery
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for setting up a battery model:
- Automation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ automation and macro features.
- Design Exploration
  The tutorials in this set illustrate various features for running design exploration studies in Design Manager.
- Coupling with CAE Codes
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for coupling with CAE codes:
- Analysis Methods
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for analysing and visualizing simulation data.
- Simcenter STAR-CCM+ In-cylinder
  The tutorials in this set illustrate features for simulating internal combustion engines in Simcenter STAR-CCM+ using the dedicated add-on Simcenter STAR-CCM+ In-cylinder.

Linear Stress Analysis: Cantilever I Beam

This tutorial demonstrates the basic concepts and workflow for linear FE (Finite Element) structural analyses in Simcenter STAR-CCM+.

The case under study is a cantilevered I beam loaded at its free end. The displacements that result from loading are assumed to be small, so that the load-displacement relationship remains linear. For simplicity, the beam is assumed weightless.

In this tutorial, you compare the numerical solution, obtained with 3D solid hexahedral elements in Simcenter STAR-CCM+, with the analytical solution given by Euler-Bernoulli beam theory. This theory is valid for slender beams with $\frac{L}{h} > 10$ .

The mathematical model is schematized below.


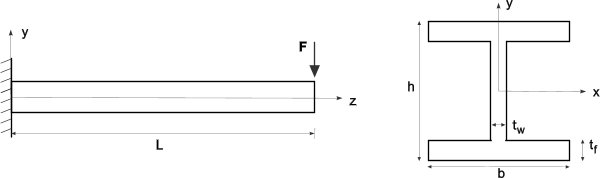
Geometry		Material Properties (Ferretic Steel)/Load
Flange thickness	$\begin{matrix} t_{f} = 8.5 m m \end{matrix}$	Load	$\| F \| = 800 N$
Web thickness	$\begin{matrix} t_{w} = 5.6 m m \end{matrix}$	Young's Modulus	$E = 2 \cdot 10^{5} M P a$
Beam height	$\begin{matrix} h = 200 m m \end{matrix}$	Poisson Ratio	$ν = 0.3$
Beam length	$\begin{array}{l} L = 4000 m m \end{array}$	Density	$ρ = 7500 k g / m^{3}$
Flange length	$\begin{matrix} b = 100 m m \end{matrix}$	Density	$ρ = 7500 k g / m^{3}$

For this problem, Bernoulli-Euler's beam theory gives the values of the deflection at the free end, and the maximum value of the stress tensor component

σ_{z z}

, as:

\begin{array}{l} δ_{y, \max} = \frac{F L^{3}}{3 E I_{x}} \approx 4.63 m m \\ σ_{z z, \max} = \frac{M}{I_{x}} \cdot \frac{h}{2} \approx 17.3 M P a \end{array}

(5264)

where

I_{x} = \int_{A} y^{2} ⅆ A \approx 1845.6 \cdot 10^{4} {m m}^{4}

is the moment of inertia about the x axis,

M

is the bending moment, and all the remaining quantities are listed in the table above.