Home
Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
Solid Stress
The tutorials in this set illustrate various Simcenter STAR-CCM+ features for computing deformation, strain, and stresses in solid regions. They also show how such computations can be coupled to the fluid behavior in an analysis of fluid-structure interaction.
FSI with Opening and Closing Flow Paths: Diaphragm Valve
Simcenter STAR-CCM+ provides the capability of performing a two-way coupled fluid-structure interaction (FSI) simulation with opening and closing flow paths, which are due to the deformation of a hyperelastic non-linear material such as rubber. This capability can aid in the design of (but is not limited to) seals, valves, and gaskets used within a range of industries.

Share

Link: copied

Breadcrumb: copied

Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
- Using Tutorial Macros and Files
  Macros, input files, and final simulation files for a range of tutorials are provided as an optional download package on the Support Center website. These macros and final simulation files are provided as an aid to the written tutorials, so that you can check your final results against the downloaded files, or against a simulation that is built and run using the macros.
- Introduction
  Welcome to the Simcenter STAR-CCM+ introductory tutorial. In this tutorial, you explore the important concepts and workflow. Complete this tutorial before attempting any others.
- Foundation Tutorials
  The foundation tutorials showcase the major features of Simcenter STAR-CCM+ in a series of short tutorials.
- Geometry
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for creating and working with parts and 3D-CAD.
- Mesh
  The tutorials in this set illustrate various STAR-CCM+ features for building CFD meshes.
- Incompressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for incompressible fluid flows as well as porosity and solution recording
- Compressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for compressible fluid flows as well as harmonic balance.
- Heat Transfer and Radiation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for heat transfer, radiation, and thermal comfort.
- Multiphase Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating multiphase fluid flow problems
- Discrete Element Method
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating Discrete Element Method problems
- Motion
  The tutorials in this set illustrate various STAR-CCM+ features for simulating problems with moving geometries and meshes, dynamic fluid body interaction, and rigid body motion:
- Reacting Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating reacting flows such as combustion.
- Solid Stress
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for computing deformation, strain, and stresses in solid regions. They also show how such computations can be coupled to the fluid behavior in an analysis of fluid-structure interaction.
  - Linear Stress Analysis: Cantilever I Beam
    This tutorial demonstrates the basic concepts and workflow for linear FE (Finite Element) structural analyses in Simcenter STAR-CCM+.
  - Plane Stress: Plate with Circular Hole in a Tensile Field
    This tutorial demonstrates how to set up a linear elastic FE (Finite Element) stress analysis in Simcenter STAR-CCM+.
  - Hyperelastic Stress Analysis with Adaptive Time-Step: Trileaflet Heart Valve
    Trileaflet valves are prosthetic heart valves that open and close because of the deformation of the flexible leaflets [reflink]. Obtaining a successful simulation of the valve opening event is challenging due to the snap through instability on which the valve operation depends. Simcenter STAR-CCM+ provides a dynamic time-step control that makes a successful simulation possible.
  - Normal Modes Solver: Wind Turbine Blade
    In solid mechanics, normal modes describe the oscillating motion of a solid body at a set of fixed frequencies, known as natural (or resonant) frequencies of the body.
  - Conjugate Heat Transfer and Thermal Stress: Exhaust Manifold
    Simcenter STAR-CCM+ allows you to combine the advantages of the finite volume (FV) and the finite element (FE) methods together in the same simulation.
  - Thermal Stress from Mapped Temperature Data: Exhaust Manifold
    This tutorial demonstrates how to perform thermal stress analysis in Simcenter STAR-CCM+.
  - Fluid-Structure Interaction: Vibrating Pipe
    This tutorial demonstrates how to set up fluid-structure interaction (FSI) problems in Simcenter STAR-CCM+.
  - FSI with Prescribed Solid Motion: Flapping Wing
    In Simcenter STAR-CCM+, you can analyse the two-way coupled fluid-structure interaction of systems whose motion paths are described by multiple superposed motions.
  - FSI and 6-DOF Motion: Stress Analysis on Boat Propeller
    In fluid-structure interaction simulations, you can define the motion of a solid structure relative to the motion of a 6-DOF body. A typical application is the analysis of the mechanical stresses on propellers attached to marine vessels.
  - FSI with Opening and Closing Flow Paths: Diaphragm Valve
    Simcenter STAR-CCM+ provides the capability of performing a two-way coupled fluid-structure interaction (FSI) simulation with opening and closing flow paths, which are due to the deformation of a hyperelastic non-linear material such as rubber. This capability can aid in the design of (but is not limited to) seals, valves, and gaskets used within a range of industries.
    - Prerequisites
      The instructions in this tutorial assume that you are already familiar with certain techniques in Simcenter STAR-CCM+.
    - Loading the Initial Simulation
      You are provided with a starting simulation that includes the required geometry, regions, interfaces, and reports. Load the initial simulation into a double precision version of Simcenter STAR-CCM+ .
    - Defining the Hyperelastic Material Continuum
      You model the rubber diaphragm with the Neo-Hookean model for hyperelastic materials. This model requires the bulk modulus and the $c_{10}$ coefficient as inputs.
    - Generating the Mesh
      The starting simulation contains predefined mesh operations. These operations generate appropriate meshes for the fluid and solid region.
    - Setting the FSI Coupling
      You define two-way coupled FSI between the solid diaphragm and the fluid overset region.
    - Applying the Constraints to the Solid Region
      To constrain the solid region, you apply four constraints.
    - Setting the Stopping Criteria
      The solid model is highly nonlinear because of the nonlinear geometry, the hyperelastic model, and the contact. To improve the stability and convergence rate of the two-way coupled fluid-structure model, you apply the Dynamic stabilization method.
    - Visualizing the Solution
      A scene has already been created to visualize the fluid velocity and the Von Mises Stress in the diaphragm. To visualize the Von Mises stress and the Plunger motion the relevant displayer properties must be defined.
    - Running the Simulation.
      Initialize the solution using the initial conditions and running the solution to convergence.
  - FSI Remeshing and Tessellated Geometry Parts Contact: Rubber Sleeve
    Simcenter STAR-CCM+ allows you to model the mechanical contact between a deformable structure and the tessellated surfaces of geometry parts within the simulation. This is useful to simulate the interaction between an elastic solid and a rigid obstacle, without modeling the obstacle explicitly.
- Aeroacoustics
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for solving aeroacoustic simulations.
- Electromagnetism
  The following tutorials illustrate features for solving problems that involve electromagnetic fields.
- Electrochemistry
  The following tutorial demonstrates chemical reactions induced by an electrical current.
- Battery
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for setting up a battery model:
- Automation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ automation and macro features.
- Design Exploration
  The tutorials in this set illustrate various features for running design exploration studies in Design Manager.
- Coupling with CAE Codes
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for coupling with CAE codes:
- Analysis Methods
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for analysing and visualizing simulation data.
- Simcenter STAR-CCM+ In-cylinder
  The tutorials in this set illustrate features for simulating internal combustion engines in Simcenter STAR-CCM+ using the dedicated add-on Simcenter STAR-CCM+ In-cylinder.

FSI with Opening and Closing Flow Paths: Diaphragm Valve

Simcenter STAR-CCM+ provides the capability of performing a two-way coupled fluid-structure interaction (FSI) simulation with opening and closing flow paths, which are due to the deformation of a hyperelastic non-linear material such as rubber. This capability can aid in the design of (but is not limited to) seals, valves, and gaskets used within a range of industries.

In this tutorial, you simulate the flow of air through a diaphragm valve. The valve consists of a hyperelastic rubber membrane that deforms in response to the fluid and a moving plunger. This response opens and closes the valve at the seal. The following screenshot shows the geometry of the diaphragm valve:

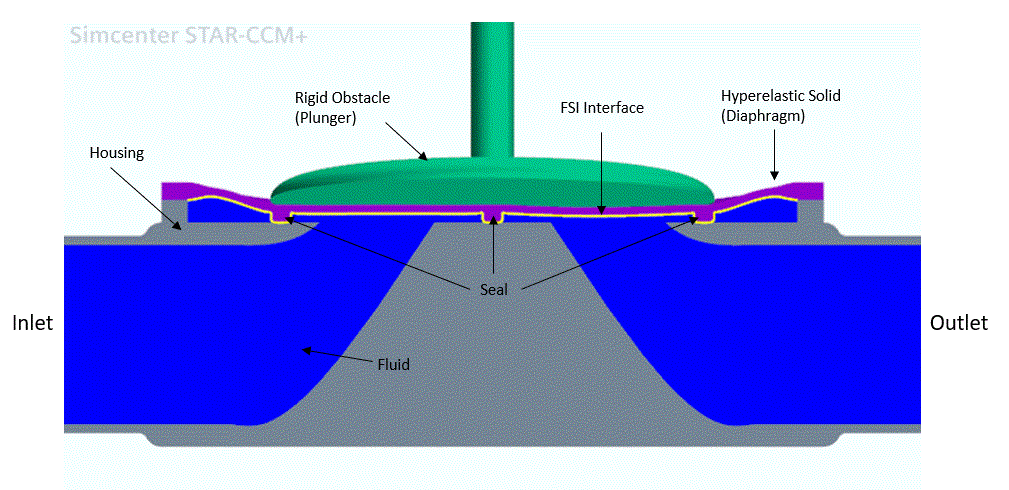
For this specific case an unsteady turbulent flow enters the passage at 0.1m/s from the inlet. The flow passes beneath the rubber diaphragm and pushes against the valve at the FSI interface. Over a period of 4 seconds the plunger moves downwards, causing the diaphragm to deform and close the flow passage between the valve and the housing. The plunger motion is defined by a translation motion in the negative z axis.

The model is split into three regions. The fluid region contains the inlet and outlet for the air flowing through the valve as well as the bypass and the gap boundary between the seal and the structure. A fluid overset region contains the volume of fluid around the deforming seal. The third region, for the solid, contains the diaphragm. To ensure that the flow path can be closed completely, an overset mesh zero gap interface is defined between the fluid region and the fluid overset region.

Two-way coupling is activated in order to model the effect of the diaphragm deformation on the flow, and to account for the impact of the flow on the diaphragm. In the coupling, the displacement field is passed from the solid to the fluid, and the fluid traction (pressure and wall shear stress) is passed from the fluid to the solid. The diaphragm itself is modeled using a hyperelastic material law and is constrained at the rim of the seal.