Home
Theory
Simcenter STAR-CCM+ simulations are built on numerical algorithms that solve relevant laws of physics according to the conditions that the simulation defines. So that you can identify the physical laws, and understand the methods by which they are solved, Simcenter STAR-CCM+ comes with a Theory Guide.
Batteries
Physics-based Models
This section introduces the physics-based battery models.
Potential Model
This section describes the Potential model.

Share

Link: copied

Breadcrumb: copied

Theory
Simcenter STAR-CCM+ simulations are built on numerical algorithms that solve relevant laws of physics according to the conditions that the simulation defines. So that you can identify the physical laws, and understand the methods by which they are solved, Simcenter STAR-CCM+ comes with a Theory Guide.
- Fundamental Equations
  Simcenter STAR-CCM+ models a range of physics phenomena including fluid mechanics, solid mechanics, heat transfer, electromagnetism, and chemical reactions. On a macroscopic scale, where the typical lengths are much greater than the inter-atomic distances, the discrete structure of matter can be neglected and materials can be modeled as continua. The mathematical models that describe the physics of continua are derived from fundamental laws that express conservation principles.
- Fluid Flow
  Simcenter STAR-CCM+ can simulate internal and external fluid flow across a wide range of flow regimes, and for a variety of fluid types. It solves the conservation equations for mass, momentum, and energy for general incompressible and compressible fluid flows.
- Numerical Flow Solution
  In the finite volume method, the solution domain is subdivided into a finite number of small control volumes, corresponding to the cells of a computational grid.
- Turbulence
- Transition
  The term transition refers to the phenomenon of laminar to turbulence transition in boundary layers. A transition model in combination with a turbulence model predicts the onset of transition in a turbulent boundary layer.
- Wall Treatment
  Walls are a source of vorticity in most flow problems of practical importance. Therefore, an accurate prediction of the flow across the wall boundary layer is essential.
- Wall Distance
  Wall distance is a parameter that represents the distance from a cell centroid to the nearest wall face with a non-slip boundary condition. Various physical models require this parameter to account for near-wall effects.
- Heat Transfer
  Heat transfer is the exchange of thermal energy between media at different temperatures. Heat transfers from locations of high temperature to locations of low temperature in order to reach an equilibrium state. The three main mechanisms of heat transfer are: conduction, convection, and radiation.
- Porous Media
  Porous media are continua that contain both fluid and fine-scale solid structures, for example: packed-bed chemical reactors, filters, radiators, honeycomb structures, or fibrous materials. The solid geometrical structures are too fine to be individually meshed and fully resolved by a computational grid.
- Species and Passive Scalars
  Simcenter STAR-CCM+ models the transport, the mixing, and the chemical reactions of multi-component liquids or multi-component gases by solving conservation equations for scalar variables that represent the mass fraction of each species in the mixture. This conservation equation allows for convection, diffusion, and optional source effects, and is solved in addition to the global mass continuity equation.
- Multiphase—Eulerian Approach
  Multiphase flows, where several fluids flow in the domain of interest, play an important role in variety of industrial applications. In general, we associate phases with gases, liquids or solids and as such some simple examples of multiphase flows are: air bubbles rising in a glass of water, sand particles carried by wind, rain drops in air. The definition of phase can be generalized and applied to other fluid characteristics such as size, shape, density, and temperature.
- Multiphase—Lagrangian Approach
  Multiphase flows are found in a wide variety of industrial processes, some examples of which are internal combustion engines, liquid, or solid fueled combustors, spray driers, cyclone dust separators, and chemical reactors. Multiphase in this context refers to one thermodynamic phase, be it a solid, a liquid, or a gas, interacting with another distinct phase.
- Reacting Flow
  In reacting flows, chemical species mix with each other and react when conditions allow. To model these flows, Simcenter STAR-CCM+ couples species and energy transport equations with the chemistry solvers that compute the source terms.
- Internal Combustion Engines
  Numerical modeling of internal combustion engines plays an increasingly important role in improving engine design. CFD simulation of such engines can give a comprehensive insight into the wide-ranging physics of the device, such as turbulent mixing between fuel and air, the ignition, and combustion chemistry.
- Electrochemistry
  Electrochemistry is the discipline investigating relationships between electrical currents and chemical composition change in general.
- Plasma
  Plasma is a state of matter similar to a gas that is composed partially or completely of charged particles such as ions and electrons which are not bound to each other.
- Electromagnetism
  Many engineering applications, such as electric motors, electric switches, and transformers, involve electromagnetic phenomena. Electromagnetic phenomena can be modeled based on the classical theory of Electromagnetism, which describes the interaction between electrically charged particles in terms of electric fields, magnetic fields, and their mutual interaction.
- Batteries
  - NTG (Newman, Tiedeman, Gu) Model
    The NTG model uses a polynomial representation to capture the voltage performance of a battery cell.
  - Thermal Runaway
  - RCR Model
    The RCR model uses a simple equivalent circuit consisting of a resistance $R_{o}$ in series with a resistor $R_{p}$ and capacitor $C$ in parallel, along with a state-of-charge dependent voltage source $V_{o}$ to represent the behavior of the battery cell.
  - Physics-based Models
    This section introduces the physics-based battery models.
    - Potential Model
      This section describes the Potential model.
    - Concentration Model
      This section describes the Concentration model.
    - Solid Electrolyte Interface Current Density
      This section describes the solid electrolyte interface current density formulation.
    - DistNP Model
      The DistNP model is an extension of the DualFoil model. The Simcenter STAR-CCM+ implementation allows for several active materials within the same model and also accounts for complex expressions to model diffusion coefficients.
    - DistSegregated Model
      The DistSegregated model is an extension of the DualFoil model. The Simcenter STAR-CCM+ implementation employs an iterative, segregated solution algorithm, but allows only a single active material per electrode. Active material particles are modeled as spheres.
  - Battery Modeling Bibliography
- Solid Mechanics
  Solid Mechanics describes the behavior of a solid continuum in response to applied loads. Applied loads include body forces, surface loads, point forces, or thermal loads that result from changes in the solid temperature. Applied loads induce a stress field in the structure and can cause displacement of the structure—from an initial undeformed configuration to a deformed configuration.
- Aeroacoustics
  Computational aeroacoustics (CAA) is a branch of multiphysics modeling and simulation that involves identifying noise sources that are induced by fluid flow and propagation of the sound waves then generated.
- Finite Element Method
  The Finite Element method is a powerful tool for finding approximate solutions to continuous problems. The methodology is similar to other numerical techniques that approximate continuous partial differential equations with discrete algebraic equations.
- Mesh Motion
  In transient simulations, mesh motion is a numerical technique that allows you to update the position of the computational domain while the solvers run.
- 6-DOF Rigid Body Motion
  Simcenter STAR-CCM+ allows you to model the motion of a rigid body in response to applied forces and moments. In a rigid body, the relative distance between internal points does not change. Therefore, it is sufficient to solve the equations of motion for the center of mass of the body.
- Rotating Flow
  Rotating flow usually occurs in rotating machinery such as pumps, propellers, fans, wind turbines, and so on.
- Harmonic Balance
  Harmonic Balance equations describe periodic unsteady flows where the unsteady frequencies are known beforehand. They are suited to modeling periodically repeating flow fields that typically occur in turbomachinery such as compressors, turbines, and fans.
- Adjoint
  The adjoint method is an efficient means to predict the influence of many input parameters on some engineering quantities of interest in a simulation.
- Design Manager
  Design Manager provides an automated approach within Simcenter STAR-CCM+ to run design exploration studies. Design exploration covers both performance assessment and optimization.
- Scalars, Vectors, and Tensors
  Most physical quantities in Simcenter STAR-CCM+ are either scalars, vectors, or 2nd-order tensors.
- Solution Data Interpolation
  Many operations require interpolation of solution data between different sets of mesh points. For example, remeshing operations require interpolation of existing solution data onto a new mesh. Data interpolation also occurs at the interface between regions, where contacting boundaries exchange data. Additionally, configurable data mappers allow you to interpolate field functions and tabular data to specified meshes.
- Idealizations
  In many simulations, it is common practice to reduce the size of the computational domain using planes of symmetry, axes of rotation, periodicity, or by reducing the 3D domain to a 2D domain. However, when you calculate physical quantities using reports you generally want to account for the whole domain. You can obtain report values for the full model using idealizations.

Potential Model

This section describes the Potential model.

Solid Active Material

Integral equation

Figure 1. EQUATION_DISPLAY

\int_{A}^{} - σ \nabla ϕ_{s} \cdot d A = - \int_{V}^{} a J_{n} d V - \int_{V}^{} a C \frac{\partial (ϕ_{s} - ϕ_{l})}{\partial t} d V

(4411)

where the terms are defined as follows:


$σ$	electrical conductivity [S/m]
$ϕ$	electric potential [V]
$a$	specific interfacial area [m²/m³]
$C$	double-layer capacitance [Farad/m²]
$J_{n}$	SEI normal component of electric current density [A/m²]

Effects introduced by surface chemistry are modeled by the terms on the right-hand side of Eqn. (4411), where the second term corresponds to the double-layer capacitance effect.

(Electric) Current definition

In the solid electrodes and current collectors, the electric current density is defined using Ohm’s law as:

Figure 2. EQUATION_DISPLAY

J_{s} = - σ \nabla ϕ_{s}

(4412)

Electrolyte

Integral equation

Figure 3. EQUATION_DISPLAY

\int_{A}^{} - κ \nabla ϕ_{l} \cdot d A = \int_{A}^{} - κ_{d} \nabla (\ln c_{l}) \cdot d A + \int_{V}^{} a J_{n} d V + \int_{V}^{} a C \frac{\partial (ϕ_{s} - ϕ_{l})}{\partial t} d V

(4413)

The effective electrical (ionic) conductivity $κ$ in the liquid phase accounts for an eventual non-unity porosity $ε$ and tortuosity $τ$ within the separator:

Figure 4. EQUATION_DISPLAY

κ = κ_{0} \frac{ε}{τ}

(4414)

Figure 5. EQUATION_DISPLAY

κ_{d} = \frac{2 R T κ}{F} (1 - {t_{+}}^{0}) [1 + \frac{d (ln f_{\pm})}{d (ln c)}]

(4415)

(Ionic) Current definition

Figure 6. EQUATION_DISPLAY

J_{l} = - κ \nabla ϕ_{l} + κ_{d} \nabla (\ln c_{l})

(4416)

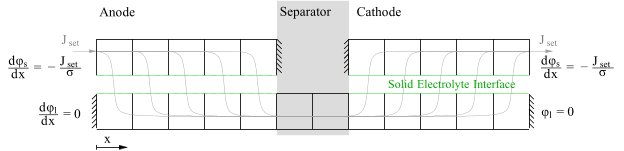
A schematic illustration describing the electric potential formulation, including the prescribed boundary conditions, is shown below: