Home
Theory
Simcenter STAR-CCM+ simulations are built on numerical algorithms that solve relevant laws of physics according to the conditions that the simulation defines. So that you can identify the physical laws, and understand the methods by which they are solved, Simcenter STAR-CCM+ comes with a Theory Guide.
Solid Mechanics
Solid Mechanics describes the behavior of a solid continuum in response to applied loads. Applied loads include body forces, surface loads, point forces, or thermal loads that result from changes in the solid temperature. Applied loads induce a stress field in the structure and can cause displacement of the structure—from an initial undeformed configuration to a deformed configuration.
Solution Methods
For compressible materials, the only unknown in the governing equations is the displacement field. For nearly incompressible materials, Simcenter STAR-CCM+ uses a two-field approach with two independent variables, the displacement field $u$ and the pressure $p$ .
Load Stepping
For cases with nonlinear geometry (large deformations) and nonlinear materials (plastic or hyperelastic solids), the governing equations can be highly nonlinear, causing the solution to diverge. To decrease the nonlinearity of the system and improve convergence, it is convenient to apply the external loads progressively over several steps.

Share

Link: copied

Breadcrumb: copied

Theory
Simcenter STAR-CCM+ simulations are built on numerical algorithms that solve relevant laws of physics according to the conditions that the simulation defines. So that you can identify the physical laws, and understand the methods by which they are solved, Simcenter STAR-CCM+ comes with a Theory Guide.
- Fundamental Equations
  Simcenter STAR-CCM+ models a range of physics phenomena including fluid mechanics, solid mechanics, heat transfer, electromagnetism, and chemical reactions. On a macroscopic scale, where the typical lengths are much greater than the inter-atomic distances, the discrete structure of matter can be neglected and materials can be modeled as continua. The mathematical models that describe the physics of continua are derived from fundamental laws that express conservation principles.
- Fluid Flow
  Simcenter STAR-CCM+ can simulate internal and external fluid flow across a wide range of flow regimes, and for a variety of fluid types. It solves the conservation equations for mass, momentum, and energy for general incompressible and compressible fluid flows.
- Numerical Flow Solution
  In the finite volume method, the solution domain is subdivided into a finite number of small control volumes, corresponding to the cells of a computational grid.
- Turbulence
- Transition
  The term transition refers to the phenomenon of laminar to turbulence transition in boundary layers. A transition model in combination with a turbulence model predicts the onset of transition in a turbulent boundary layer.
- Wall Treatment
  Walls are a source of vorticity in most flow problems of practical importance. Therefore, an accurate prediction of the flow across the wall boundary layer is essential.
- Wall Distance
  Wall distance is a parameter that represents the distance from a cell centroid to the nearest wall face with a non-slip boundary condition. Various physical models require this parameter to account for near-wall effects.
- Heat Transfer
  Heat transfer is the exchange of thermal energy between media at different temperatures. Heat transfers from locations of high temperature to locations of low temperature in order to reach an equilibrium state. The three main mechanisms of heat transfer are: conduction, convection, and radiation.
- Porous Media
  Porous media are continua that contain both fluid and fine-scale solid structures, for example: packed-bed chemical reactors, filters, radiators, honeycomb structures, or fibrous materials. The solid geometrical structures are too fine to be individually meshed and fully resolved by a computational grid.
- Species and Passive Scalars
  Simcenter STAR-CCM+ models the transport, the mixing, and the chemical reactions of multi-component liquids or multi-component gases by solving conservation equations for scalar variables that represent the mass fraction of each species in the mixture. This conservation equation allows for convection, diffusion, and optional source effects, and is solved in addition to the global mass continuity equation.
- Multiphase—Eulerian Approach
  Multiphase flows, where several fluids flow in the domain of interest, play an important role in variety of industrial applications. In general, we associate phases with gases, liquids or solids and as such some simple examples of multiphase flows are: air bubbles rising in a glass of water, sand particles carried by wind, rain drops in air. The definition of phase can be generalized and applied to other fluid characteristics such as size, shape, density, and temperature.
- Multiphase—Lagrangian Approach
  Multiphase flows are found in a wide variety of industrial processes, some examples of which are internal combustion engines, liquid, or solid fueled combustors, spray driers, cyclone dust separators, and chemical reactors. Multiphase in this context refers to one thermodynamic phase, be it a solid, a liquid, or a gas, interacting with another distinct phase.
- Reacting Flow
  In reacting flows, chemical species mix with each other and react when conditions allow. To model these flows, Simcenter STAR-CCM+ couples species and energy transport equations with the chemistry solvers that compute the source terms.
- Internal Combustion Engines
  Numerical modeling of internal combustion engines plays an increasingly important role in improving engine design. CFD simulation of such engines can give a comprehensive insight into the wide-ranging physics of the device, such as turbulent mixing between fuel and air, the ignition, and combustion chemistry.
- Electrochemistry
  Electrochemistry is the discipline investigating relationships between electrical currents and chemical composition change in general.
- Plasma
  Plasma is a state of matter similar to a gas that is composed partially or completely of charged particles such as ions and electrons which are not bound to each other.
- Electromagnetism
  Many engineering applications, such as electric motors, electric switches, and transformers, involve electromagnetic phenomena. Electromagnetic phenomena can be modeled based on the classical theory of Electromagnetism, which describes the interaction between electrically charged particles in terms of electric fields, magnetic fields, and their mutual interaction.
- Batteries
- Solid Mechanics
  Solid Mechanics describes the behavior of a solid continuum in response to applied loads. Applied loads include body forces, surface loads, point forces, or thermal loads that result from changes in the solid temperature. Applied loads induce a stress field in the structure and can cause displacement of the structure—from an initial undeformed configuration to a deformed configuration.
  - Displacement
    Applied loads can result in a displacement of the solid structure from an initial configuration to a deformed configuration. The total displacement is a combination of rigid body motion and the relative displacements of the points in the body, which determine the deformation of the solid structure.
  - Stress
    Stress is a measure of the force per unit area acting on a surface. In a solid structure, external forces or temperature changes induce a stress field, which can lead to motion and deformation of the solid structure. Internal forces that oppose the deformation of the structure also induce an internal elastic stress that tends to restore the structure to the original undeformed state. Some materials also present built-in stress, that exists in absence of applied forces and deformations.
  - Strain
    Strain is a measure of the deformation of a body in terms of the relative displacement of its material points.
  - Governing Equations
    Solid Mechanics studies the displacement of a solid continuum under prescribed loads and constraints. The fundamental laws that govern the mechanics of solids are the same laws that describe the mechanics of fluids, namely, the conservation of mass, linear momentum, angular momentum, and energy.
  - Inertial Loads
    Deformable bodies undergoing rigid body motions are subject to inertial loads. To model these phenomena correctly it is convenient to separate rigid displacements due to rigid motion from non-rigid displacements due to the deformation of the solid.
  - Contact with a Rigid Surface
    A rigid contact constraint defines a boundary condition on the surface of a deformable solid. This boundary condition accounts for the contact between the solid and a rigid surface that is not part of the stress analysis.
  - Constitutive Relations: Material Models
    The strain tensor is directly related to the gradient of the displacement, whereas the stress tensor is related to the displacement through the strain tensor. Constitutive relations complete the formulation by describing the relationship between stress and strain.
  - Finite Element Discretization
    Simcenter STAR-CCM+ calculates the displacement of a solid based on the principle of virtual work, which is discretized using the Finite Element method.
  - Rayleigh Damping
    The formulation presented in the previous sections does not take into account the damping mechanisms that arise in time-dependent systems. Damping is the dissipation of energy in the solid structure due to a combination of different phenomena, including molecular interaction within the material.
  - Solution Methods
    For compressible materials, the only unknown in the governing equations is the displacement field. For nearly incompressible materials, Simcenter STAR-CCM+ uses a two-field approach with two independent variables, the displacement field $u$ and the pressure $p$ .
    - Load Stepping
      For cases with nonlinear geometry (large deformations) and nonlinear materials (plastic or hyperelastic solids), the governing equations can be highly nonlinear, causing the solution to diverge. To decrease the nonlinearity of the system and improve convergence, it is convenient to apply the external loads progressively over several steps.
    - Anderson Acceleration
      The Anderson acceleration method, also known as the Quasi-Newton Inverse Least Squares method, is a solution stabilization method for strongly coupled FSI applications. This method can accelerate convergence and improve the stability of the solution.
  - Normal Modes
    A normal mode is an undamped, sinusoidal motion pattern over time at a fixed frequency. The structure remains in dynamic equilibrium and undergoes a free vibration. The normal modes and natural frequencies of a structure govern its dynamic response.
  - Bibliography
- Aeroacoustics
  Computational aeroacoustics (CAA) is a branch of multiphysics modeling and simulation that involves identifying noise sources that are induced by fluid flow and propagation of the sound waves then generated.
- Finite Element Method
  The Finite Element method is a powerful tool for finding approximate solutions to continuous problems. The methodology is similar to other numerical techniques that approximate continuous partial differential equations with discrete algebraic equations.
- Mesh Motion
  In transient simulations, mesh motion is a numerical technique that allows you to update the position of the computational domain while the solvers run.
- 6-DOF Rigid Body Motion
  Simcenter STAR-CCM+ allows you to model the motion of a rigid body in response to applied forces and moments. In a rigid body, the relative distance between internal points does not change. Therefore, it is sufficient to solve the equations of motion for the center of mass of the body.
- Rotating Flow
  Rotating flow usually occurs in rotating machinery such as pumps, propellers, fans, wind turbines, and so on.
- Harmonic Balance
  Harmonic Balance equations describe periodic unsteady flows where the unsteady frequencies are known beforehand. They are suited to modeling periodically repeating flow fields that typically occur in turbomachinery such as compressors, turbines, and fans.
- Adjoint
  The adjoint method is an efficient means to predict the influence of many input parameters on some engineering quantities of interest in a simulation.
- Design Manager
  Design Manager provides an automated approach within Simcenter STAR-CCM+ to run design exploration studies. Design exploration covers both performance assessment and optimization.
- Scalars, Vectors, and Tensors
  Most physical quantities in Simcenter STAR-CCM+ are either scalars, vectors, or 2nd-order tensors.
- Solution Data Interpolation
  Many operations require interpolation of solution data between different sets of mesh points. For example, remeshing operations require interpolation of existing solution data onto a new mesh. Data interpolation also occurs at the interface between regions, where contacting boundaries exchange data. Additionally, configurable data mappers allow you to interpolate field functions and tabular data to specified meshes.
- Idealizations
  In many simulations, it is common practice to reduce the size of the computational domain using planes of symmetry, axes of rotation, periodicity, or by reducing the 3D domain to a 2D domain. However, when you calculate physical quantities using reports you generally want to account for the whole domain. You can obtain report values for the full model using idealizations.

Load Stepping

For cases with nonlinear geometry (large deformations) and nonlinear materials (plastic or hyperelastic solids), the governing equations can be highly nonlinear, causing the solution to diverge. To decrease the nonlinearity of the system and improve convergence, it is convenient to apply the external loads progressively over several steps.

Considering the static nonlinear problem:

Figure 1. EQUATION_DISPLAY

\begin{matrix} r (u) : = f_{int} - f_{e x t} \end{matrix} = 0

(4627 4628 4631)

With load stepping, Eqn. (4627) can be written as:

Figure 2. EQUATION_DISPLAY

\begin{matrix} r (u^{s}) : = f_{int} - λ^{s} f_{e x t} \end{matrix} = 0

(4627 4628 4631)

where the stepping factor $λ^{s}$ accounts for the ramping of the load over the steps $s$ . Currently, Simcenter STAR-CCM+ uses the load loop approach. With this approach, the external load is split into parts which are incrementally applied in separate load steps. In each load step, the nonlinear sytem Eqn. (4627) is solved with the Newton-Raphson method:

Figure 3. EQUATION_DISPLAY

u_{k + 1}^{s} = u^{s - 1} + Δ u_{k + 1}^{s}

(4629 4630)

Figure 4. EQUATION_DISPLAY

Δ u_{k + 1}^{s} = Δ u_{k}^{s} + d u

(4629 4630)

Figure 5. EQUATION_DISPLAY

\begin{matrix} r (u_{k + 1}^{s}) = f_{int} (u_{k + 1}^{s}) - λ^{s} f_{e x t} \end{matrix} = 0

(4627 4628 4631)

Linear Load Stepping

The Linear Load Step Control applies the load increment at each step based on the convergence of the previous load steps. If the current load step is:

The first load step of the simulation, then the user-defined Initial load increment is used.
The first load step of the time-step, then all load steps of the first load loop of the previous time-step are considered.
The first load step of a load loop, then all load steps of the previous load loop are considered.
A subsquent step of a load loop, then all load steps of the current load loop are considered.

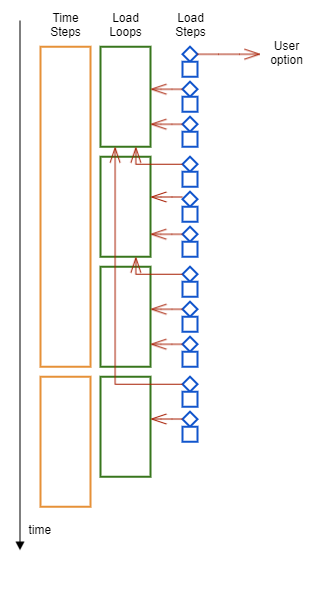
The following diagram illustrates the above conditions:

At each load step the solver increments the load linearly using a least squares method:

a = \frac{\sum_{i} x_{i} y_{i}}{\sum_{i} x_{i} x_{i}}

(4632)

x = \frac{y}{a}

(4633)

Where

y

is the optimal number of newton steps,

x

is the load step size of the next load step,

y_{i}

is the number of iterations of a previous load step

i

, and,

x_{i}

is the load step size of a previous load step

i

.