Algebraic Multigrid

Simcenter STAR-CCM+ provides two methods for accelerating the linear solver, the preconditioned conjugate-gradient method for incompressible flows and the bi-conjugate gradient stabilized method for all others.

Multigrid Cycling

Multigrid techniques enable a basic iteration scheme such as Gauss-Seidel to be greatly accelerated by using simple correction sweeps on a sequence of coarse meshes. The strategy for visiting the coarse levels can have a significant impact on the efficiency of the algorithm. Two cycling strategies are available in the AMG solver that is used in Simcenter STAR-CCM+—fixed and flexible:

• Fixed cycles—A complete multigrid cycle represents the recursive application of a single cycle that is composed of the following steps:
  1. (Pre)smooth
  2. Restrict
  3. Cycle anew
  4. Prolongate
  5. (Post)smooth

  These steps are applied to a sequence of successively coarser grids or equation sets. Smooth means to apply any number of iterative relaxation sweeps to the equations on the current fine level to compute a new set of corrections. Restrict is to transfer the existing residuals down to the next coarsest level where a new cycle is applied. Following that the resultant corrections are prolongated—transferred back up to the current fine level—where smoothing is again applied.

  The three types of fixed cycles are:

  • F fixed cycles
  • V fixed cycles
  • W fixed cycles
• Flexible cycles—This type of cycle is a more economical cycling strategy for linear systems that are not stiff. Rather than using all multigrid levels in a regular pattern, the residuals are monitored after every sweep on a given grid level. If the residual rate of reduction exceeds a given threshold, the solution continues on a coarser level. If the residual on a given level is reduced more than a specified tolerance, the solution moves to a finer level. A limit is further imposed on the number of sweeps that are allowed at any level.

F Cycle

The F cycle is a variant of the W cycle. Illustrated below, this cycle involves fewer coarse-level sweeps than the W cycle, but still more than the V cycle.

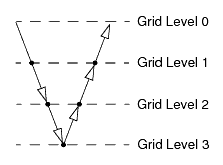
V Cycle

The V cycle is the simplest type of fixed cycle, and only has two legs. In the first leg, one performs a number of relaxation sweeps on the finest level and transfers the residuals to the next level. Then, the operation is repeated on successively coarse levels until the coarsest level is reached. A coarse “grid” generally contains only a few “cells”. After finishing the sweeps on the coarsest level, the solution is used to correct the solution on the next finer level. Some relaxation sweeps are performed on that level before repeating the process until the finest level is reached. This procedure is illustrated below.

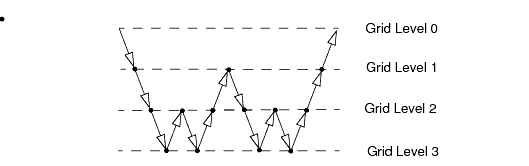
W Cycle

For stiff systems, the V cycle sometimes is not sufficient, and more coarse iterations are advantageous. The W cycle increases the number of coarse relaxation sweeps as illustrated below.

AMG Solver

The result of the discretization approach that is described above is a linear system:

representing the algebraic equations for each computational cell. The matrix $\mathbf{\text{A}}$ represents the coefficients of the linear system (for example, the coefficients $a_p$ and $a_n$ on the left-hand side of Eqn. (920), the vector $\mathbf{\text{x}}$ represents the unknowns ( $\Delta \varphi$ in Eqn. (920)) in each cell, and the vector $\mathbf{\text{b}}$ represents the residuals (see Eqn. (921)) from each cell.

The resultant linear system of equations is solved using either the Jacobi, the Gauss-Seidel, or the Incomplete Lower Upper decomposition relaxation scheme (smoother).

Jacobi and Gauss-Seidel

The general principle behind iterative methods is that, given an approximate solution ${\mathbf{\text{x}}}^k$ , a better approximation ${\mathbf{\text{x}}}^{k+1}$ is sought, and then the process is repeated.

If the error at iteration k is defined as:

$${\mathbf{\text{e}}}^k=\mathbf{\text{x}}-{\mathbf{\text{x}}}^k$$

(978)

where $\mathbf{\text{x}}$ represents the exact solution and the residual as:

$${\mathbf{\text{r}}}^k=\mathbf{\text{b}}-{\mathbf{\text{Ax}}}^k$$

(979)

it follows that:

$${\mathbf{\text{A}}\mathbf{\text{e}}}^k={\mathbf{\text{r}}}^k$$

(980)

Therefore, continuing the iteration until the residual is driven to a small value, drives the error a small value.

The most basic iterative methods are Jacobi and Gauss-Seidel iteration. These methods involve visiting each cell in sequence, and updating the value of $x_i$ in each cell i using the coefficients of its n neighbor cells as follows:

$$x_i=\frac{1}{A_{i,i}}(b-{\sum }_{\text{neighbors }n}^{}{A}_{i,n}{x}_n)$$

(981)

The difference between Jacobi and Gauss-Seidel iteration is subtle: Jacobi uses the “old” values of $x_n$ , while Gauss-Seidel uses the available values that have been updated, resulting in better convergence.

Incomplete Lower Upper (ILU)

The ILU (Incomplete Lower-Upper) method, Saad [283], solves iteratively for ${\mathbf{\text{x}}}^{k+1}$ using:

$$\widetilde{\mathbf{\text{A}}}\left({\mathbf{\text{x}}}^{k+1}-{\mathbf{\text{x}}}^k\right)=b-\mathbf{\text{A}}{\mathbf{\text{x}}}^k$$

(982)

where

$$\widetilde{\mathbf{\text{A}}}=\mathbf{\text{L}}\mathbf{\text{U}}=(\mathbf{\text{D}}+{\mathbf{\text{L}}}_A)(\mathbf{\text{I}}+{\mathbf{\text{D}}}^{-1}{\mathbf{\text{U}}}_A)$$

(983)

where $\mathbf{\text{I}}$ is the identity matrix, ${\mathbf{\text{L}}}_A$ and ${\mathbf{\text{U}}}_A$ are the lower and upper triangular matrices of the original matrix $\mathbf{\text{A}}$ , and $\mathbf{\text{D}}$ is a diagonal matrix that is calculated using the MILU(0) method.

The ILU method is more computationally expensive but more robust than the Gauss-Seidel method. The robustness of the ILU method means that it can handle group sizes of 8 or more in three dimensions; the Gauss-Seidel method can only handle group sizes of 4. Use the ILU method for complex problems, and to improve convergence and parallel scalability. For three-dimensional problems, use it with a group size of 8.

Acceleration Methods

Preconditioned Conjugate-Gradient Method

To accelerate the convergence of the iterative solution of the linear system in the Pressure solver, a conjugate-gradient method is available that uses the AMG solver as the preconditioner. Use this method for incompressible flows (Constant Density model) with the Segregated Flow model.

To solve the linear system $\mathbf{\text{A x }}=\mathbf{\text{b}}$ , the preconditioned conjugate-gradient (PCG) takes the following form:

$${\mathbf{\text{r}}}_0=\mathbf{\text{b}}-{\mathbf{\text{Ax}}}_0$$

(984)

$${\mathbf{\text{z}}}_0\cong \text{AMG fixed cycle }(\mathbf{\text{A}},{\mathbf{\text{r}}}_0)$$

(985)

$${\mathbf{\text{p}}}_0={\mathbf{\text{z}}}_0$$

(986)

$$\mathbf{\text{k}}=0$$

(987)

Each iteration involves the calculations in Eqn. (988) through Eqn. (994):

$${\alpha }_k=\frac{\left({\mathbf{\text{r}}}_k^T{\mathbf{\text{z}}}_k\right)}{\left({\mathbf{\text{p}}}_k^T\text{A}{\mathbf{\text{p}}}_k\right)}$$

(988)

$${\mathbf{\text{x}}}_{k+1}={\mathbf{\text{x}}}_k+{\alpha }_k{\mathbf{\text{p}}}_k$$

(989)

$${\mathbf{\text{r}}}_{k+1}={\mathbf{\text{r}}}_k-{\alpha }_k\mathbf{\text{A}}{\mathbf{\text{p}}}_k$$

(990)

If $\left|{\mathbf{\text{r}}}_{k+1}\right|<\epsilon$ , then the iteration ends.

$${\mathbf{\text{z}}}_{k+1}\cong \text{AMG fixed cycle }(\mathbf{\text{A}},{\mathbf{\text{r}}}_{k+1})$$

(991)

$${\beta }_k=\frac{\left({\mathbf{\text{r}}}_k^{+}{\mathbf{\text{z}}}_{k+1}\right)}{\left({\mathbf{\text{r}}}_k{\mathbf{\text{z}}}_k\right)}$$

(992)

$${\mathbf{\text{p}}}_{k+1}={\mathbf{\text{z}}}_{k+1}+{\beta }_k{\mathbf{\text{r}}}_k$$

(993)

$$k=k+1$$

(994)

The solution of the linear system is ${\mathbf{\text{x}}}_{k+1}$ .

A necessary condition for the convergence of the PCG algorithm is that the matrix $\mathbf{\text{A}}$ (which here is also the preconditioner) is symmetric positive-definite (SPD). The matrix of the linear system of the Pressure solver in pure incompressible cases satisfies this condition.

Eqn. (985) and Eqn. (991) in the iteration process are preconditioner solver calculations, which involve one AMG fixed-cycle loop to approximate the auxiliary linear systems:

$${\mathbf{\text{Az}}}_k={\mathbf{\text{r}}}_k\text{ k}=0,1,\dots$$

(995)

As implemented, the PCG accelerates convergence and improves the parallel scalability of the Pressure solver. For normal cases (no non-linear instability), it is expected that the PCG does not change significantly the overall non-linear convergence of Simcenter STAR-CCM+. The PCG can provide robust convergence for those cases where numerical instability results from a lack of incomplete convergence of the linear system of the Pressure solver.

Bi-Conjugate Gradient Stabilized Method

The Bi-Conjugate Gradient Stabilized (BiCGStab) method has been developed to solve nonsymmetric (general) linear systems. Simcenter STAR-CCM+ implements an AMG-preconditioned BiCGStab algorithm to improve the robustness and the speed of convergence of linear systems that the solvers produce.

To solve the general linear system $\mathbf{\text{A x }}=\mathbf{\text{b}}$ , the preconditioned BiCGStab takes the following steps:

$${\mathbf{\text{r}}}_0=\mathbf{\text{b}}-{\mathbf{\text{Ax}}}_0$$

(996)

$$\tilde{\text{r}}={\mathbf{\text{r}}}_0$$

(997)

$$i=0$$

(998)

Each iteration $i$ involves calculations of Eqn. (999) through Eqn. (1012):

$${\rho }_{i-1}={\tilde{\text{r}}}^T{\mathbf{\text{r}}}_{i-1}$$

(999)

If ${\rho }_{i-1}=0$ , the method fails.

If $i=1$ :

$${\mathbf{\text{p}}}_i={\mathbf{\text{r}}}_{i-1}$$

(1000)

Otherwise, as per Eqn. (1001) and Eqn. (1002):

$${\beta }_{i-1}=\left(\frac{{\rho }_{i-1}}{{\rho }_{i-2}}\right)\left(\frac{{\alpha }_{i-1}}{{\omega }_{i-1}}\right)$$

(1001)

$${\mathbf{\text{p}}}_i={\mathbf{\text{r}}}_{i-1}+{\beta }_{i-1}\left({\mathbf{\text{p}}}_{i-1}-{\omega }_{i-1}{\mathbf{\text{v}}}_{i-1}\right)$$

(1002)

$$\hat{\text{p}}=\text{AMG fixed cycle }(\mathbf{\text{A}},{\mathbf{\text{p}}}_i)$$

(1003)

$${\mathbf{\text{v}}}_i=\mathbf{\text{A}}\cdot \hat{\text{p}}$$

(1004)

$${\alpha }_i=\frac{{\rho }_{i-1}}{({\tilde{\text{r}}}^T\cdot {\mathbf{\text{v}}}_i)}$$

(1005)

$$\mathbf{\text{S}}={\mathbf{\text{r}}}_{i-1}-({\alpha }_i\cdot {\mathbf{\text{v}}}_i)$$

(1006)

If $(\left|\mathbf{\text{S}}\right|<\epsilon )$ , then as per Eqn. (1007):

$${\mathbf{\text{x}}}_i={\mathbf{\text{x}}}_{i-1}+{\alpha }_i\hat{\text{p}}$$

(1007)

and the iteration ends.

Otherwise the iteration continues as follows:

$$\hat{\text{S}}=\text{AMG fixed cycle }(\mathbf{\text{A}},\mathbf{\text{S}})$$

(1008)

$$\mathbf{\text{t}}=\text{A}\cdot \hat{\text{S}}$$

(1009)

$${\omega }_i=\frac{{\mathbf{\text{t}}}^T\cdot \mathbf{\text{S}}}{{\mathbf{\text{t}}}^T\cdot \mathbf{\text{t}}}$$

(1010)

$${\text{x}}_i={\mathbf{\text{x}}}_{i-1}+{\alpha }_i\hat{\text{p}}+{\omega }_i\mathbf{\text{S}}$$

(1011)

$${\mathbf{\text{r}}}_i=\mathbf{\text{S}}-{\omega }_i\mathbf{\text{t}}$$

(1012)

If $\left|{\mathbf{\text{r}}}_i\right|<\epsilon$ , then the iteration ends.

If ${\omega }_i\ne 0$ , then the iteration continues.

The solution of the linear system is ${\mathbf{\text{x}}}_i$ .

Eqn. (1003) and Eqn. (1008) in the iteration process are the preconditioner solver calculations, which involve one AMG fixed-cycle loop to obtain an approximate solution of:

$$\mathbf{\text{A}}\cdot \hat{\text{p}}={\mathbf{\text{p}}}_i\text{ and }\text{A}\cdot \hat{\text{S}}=\text{S}\text{ respectively}$$

(1013)

As with the Preconditioned Conjugate-Gradient method, BiCGStab can improve parallel scalability and improve robustness for those cases where numerical instability was due to lack of sufficient convergence of the linear system.

Preconditioned Generalized Minimal Residual Method

Similarly to the Preconditioned Bi-Conjugate Gradient Stabilized method, the Generalized Minimal Residual Method (GMRes) method can solve general, not necessarily symmetric, linear systems. Simcenter STAR-CCM+ implements an AMG-preconditioned GMRes algorithm to improve the robustness and the speed of convergence of the linear systems that the solvers produce, following [283], chapter 9.3.1.

Note that, compared to the Preconditioned Conjugate-Gradient and Bi-Conjugate Gradient Stabilized methods, the preconditioned GMRes method has increased memory requirements.