Finite Volume Discretization

General Transport Equation

When the appropriate constitutive relations are introduced into the conservation equations a closed set of equations is obtained. All conservation equations can be written in terms of a generic transport equation. By integrating the generic transport equation over a control volume $V$ and applying Gauss's divergence theorem, the following integral form of the transport equation is obtained:

where $\varphi$ represents the transport of a scalar property, $A$ is the surface area of the control volume and $da$ denotes the surface vector. By setting $\varphi$, for example, equal to $1,u,v,w,E,\phantom{\square }\text{or}H,Y_i$ and selecting appropriate values for the diffusion coefficient $\mathrm{\Gamma }$ and source terms, special forms of the partial differential equations for mass, momentum, energy, and species conservation are obtained.

The following diagram shows two polyhedral computational cells that illustrate the discretization of the generic transport equation:

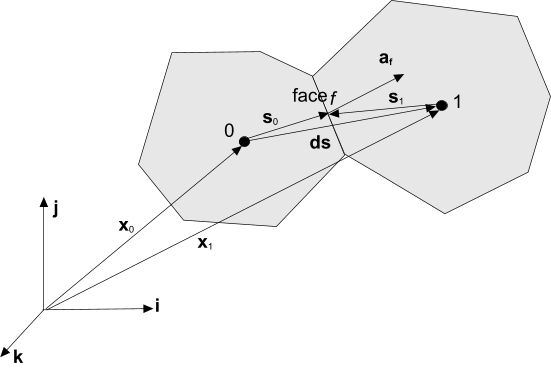
Surface Integrals

The surface integrals in Eqn. (879) are evaluated on two levels using quadrature approximations:

• The integral is expressed in terms of variable values at one location on the cell face.

  Simcenter STAR-CCM+ employs the second-order midpoint rule, that is, the integral is evaluated as the product of the value at the cell face center and the cell face area:

  $${\int }_A{J}^{\varphi }\cdot da\approx \sum _f{J}_f^{\varphi }\cdot a_f$$

  where $J^{\varphi }$ is either the convective or the diffusive flux of fluid property $\varphi$, $a_f$ is the surface area vector of face $f$ of the cell, and $\sum _f$ is the sum over all cell faces of the cell.

• The values at the cell face center are not known and are approximated through interpolation in terms of the values at the cell centers. These interpolation schemes, that is, discretization schemes are described under Convective Flux and Diffusive Flux.

Volume Integrals

The source term in Eqn. (879) requires integration over the volume of the cell. Simcenter STAR-CCM+ approximates the volume integral by the product of the mean value of the source term at the cell center and the volume of the cell. This approximation is second-order accurate.

$${\int }_V{S}_{\varphi }dV\approx S_{{\varphi }_0}{V}_0$$

(880)

To achieve second-order accuracy of these approximations, the cell face center is the area weight center and the cell center is the volume center.

Applying the integration approximations to Eqn. (879) yields the following semi-discrete transport equation:

Convective Flux

The discretized convective term at a face can be rearranged as follows:

where ${\dot{m}}_f$ is the mass flow rate at the face.

Eqn. (882) requires the values of fluid property ${\varphi }_f$ at the face. The manner in which the fluid property face value ${\varphi }_f$ is computed from the cell values has a profound effect on the stability and accuracy of the numerical scheme.

The Normalized Variable Diagram

The normalized variable diagram (NVD) is useful for analyzing boundedness properties of convective discretization schemes.

Part (a) of the figure below shows three cells in the vicinity of a cell face f, across which the velocity ${\mathbf{\text{v}}}_f$ is known. The nodal variable values are labeled ${\alpha }_D$, ${\alpha }_C$ and ${\alpha }_U$, representing the downwind, central, and upwind positions relative to each other.

The convection boundedness criterion is shown in the NVD diagram as Part (b) of the diagram:

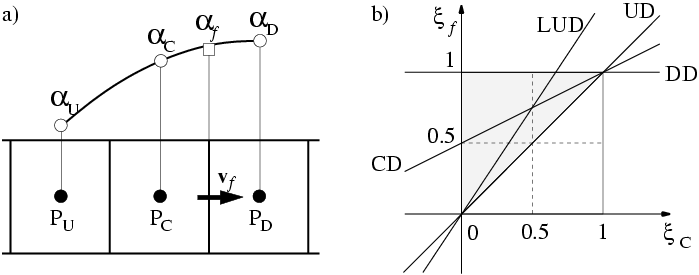
The normalized variable $\xi (\mathbf{\text{r}},t)$ in the vicinity of face f is defined as:

$$\xi (\mathbf{\text{r}},t)=\frac{\alpha (\mathbf{\text{r}},t)-{\alpha }_U}{{\alpha }_D-{\alpha }_U}$$

(883)

The normalized face value:

$${\xi }_f=\frac{{\alpha }_f-{\alpha }_U}{{\alpha }_D-{\alpha }_U}$$

(884)

calculated by any differencing scheme that uses only nodal values of $\alpha$ at points U, C, and D, can be written in the form:

$${\xi }_f={\xi }_f\left({\xi }_C\right)$$

where:

$${\xi }_C=\frac{{\alpha }_C-{\alpha }_U}{{\alpha }_D-{\alpha }_U}$$

(885)

To avoid non-physical oscillations in the solution, ${\alpha }_C$ (and consequently ${\alpha }_f$) has to be locally bounded between ${\alpha }_U$ and ${\alpha }_D$, meaning:

$${\alpha }_U\le {\alpha }_C\le {\alpha }_D$$

(886)

or

$${\alpha }_D\le {\alpha }_C\le {\alpha }_U$$

(887)

If this criterion is satisfied at every point in the domain, the entire solution is free of non-physical oscillations.

The boundedness criterion for convection differencing schemes can be presented in the NVD diagram, showing ${\xi }_f$ as a function of ${\xi }_C$, as the hatched region in part (b) of the above Figure (including the line ${\xi }_f={\xi }_C$). It can also be expressed through the following conditions:

• For ${0\le \xi }_C\le 1$ the bounded region lies above the line ${\xi }_f={\xi }_C$ and below ${\xi }_f=1$.
• For ${\xi }_C<0$ and ${\xi }_C>1$, ${\xi }_f$ is equal to ${\xi }_C$.

NVD is concerned with convective transport alone. If sources or sinks are present, the conditions that are given in Eqn. (886) and Eqn. (887) can be violated. The importance of the boundedness criterion is especially clear in the case of variables which have physical bounds; for example, the phase volume fraction cannot become negative, or larger than unity.

First-Order Upwind

The first-order upwind differencing scheme (FOU) approximates the cell face value ${\varphi }_f$ in the form of a step function. The approximation is of first-order accuracy. Depending on the flow direction, the convective flux is computed as:

$${\left(\dot{m}\varphi \right)}_f=\{\begin{array}{c}{\dot{m}}_f{\varphi }_0\text{for }{\dot{m}}_f\ge 0\\ {\dot{m}}_f{\varphi }_1\text{for }{\dot{m}}_f<0\end{array}$$

(888)

where a positive mass flux is leaving the cell and a negative mass flux is entering the cell. This discretization scheme is based on transport properties of the flow: due to convection, $\varphi$ is transported only downstream. If the streamlines of the flow are aligned with the mesh lines, the resulting approximations are good. However, if the streamlines form an angle with the mesh lines, the UDS is inaccurate. These errors are called artificial or numerical diffusion. The advantage of UDS is that it is unconditionally bounded, which is stabilizing and helps the solver achieve robust convergence. It is fairly common practice to obtain an initial solution using the first-order convection and then switch to the second-order one to obtain a more accurate, final converged solution.

Second-Order Upwind

For a second-order upwind (SOU) scheme, the convective flux is computed as:

$${\left(\dot{m}\varphi \right)}_f=\{\begin{array}{c}{\dot{m}}_f{\varphi }_{f,0}\text{for }{\dot{m}}_f\ge 0\\ {\dot{m}}_f{\varphi }_{f,1}\text{for }{\dot{m}}_f<0\end{array}$$

(889)

where the face values ${\varphi }_{f,0}$ and ${\varphi }_{f,1}$ , are linearly interpolated from the cell center values on either side of the face:

$$\begin{array}{ccc}{\varphi }_{f,0}& =& {\varphi }_0+{\mathbf{\text{s}}}_0\cdot {\left(\nabla \varphi \right)}_{r,0}\\ {\varphi }_{f,1}& =& {\varphi }_1+{\mathbf{\text{s}}}_1\cdot {\left(\nabla \varphi \right)}_{r,1}\end{array}$$

where:

$$\begin{array}{ccc}{\mathbf{\text{s}}}_0& =& {\mathbf{\text{x}}}_f-{\mathbf{\text{x}}}_0\\ {\mathbf{\text{s}}}_1& =& {\mathbf{\text{x}}}_f-{\mathbf{\text{x}}}_1\end{array}$$

The gradients ${\left(\nabla \varphi \right)}_{r,0}$ and ${\left(\nabla \varphi \right)}_{r,1}$ of cells 0 and 1 are calculated according to Eqn. (911) as limited reconstruction gradients.

Central-Differencing

The central-differencing scheme (CDS) approximates the cell face center value by linear interpolation between the two nearest neighbouring cell center values.

For a central-differencing scheme, the convective flux is computed as:

$${\left(\dot{m}\varphi \right)}_f={\dot{m}}_f[f{\varphi }_0+\left(1-f\right){\varphi }_1]$$

(890)

where the linear interpolation factor is defined as:

$$f=\frac{V_1}{V_0+V_1}$$

$f$ is related to the mesh stretching. For a uniform mesh, $f$ has a value of 0.5.

Central-differencing is formally second-order accurate. However it is prone to dispersive error and is beset with stability problems for most steady-state situations. The dispersive errors make it problematic for discretizing positive-definite quantities (such as temperature or turbulent kinetic energy) where overshoots cannot be tolerated.

A significant advantage of central-differencing over second-order upwind is that, when used to discretize velocity (not a positive definite quantity) it preserves turbulent kinetic energy. Therefore, it is a useful scheme in large eddy simulation (LES), where upwind schemes cause turbulent kinetic energy to decay unnaturally fast.

Bounded Central-Differencing

For a bounded central-differencing scheme as described in [232] and [258], the convective flux is computed as:

$${\left(\dot{m}\varphi \right)}_f=\{\begin{array}{cc}\dot{m}{\varphi }_{FOU}\hfill & \text{for}\xi <0\text{ or }1<\xi \hfill \\ \dot{m}(\sigma {\varphi }_{CD}+(1-\sigma \left){\varphi }_{SOU}\right)\hfill & \text{for }0\le \xi \le 1\hfill \end{array}$$

(891)

where:

${\varphi }_{FOU}$	Cell-face center value obtained through first-order upwind interpolation
${\varphi }_{SOU}$	Cell-face center value obtained through second-order upwind interpolation
${\varphi }_{CD}$	Cell-face center value obtained through central-differencing interpolation
$\xi$	Normalized-Variable Diagram (NVD) value that is computed based on local conditions

A smooth and monotone function of $\xi$ is:

$$\sigma =\sigma \left(\xi \right)$$

(892)

which satisfies $\sigma \left(0\right)=0$ and $\sigma \left(\xi \right)=1$ for ${\xi }_{ubf}\le \xi$ . ${\xi }_{ubf}$ is called the upwind blending factor whose value ensures a proper balance between the accuracy and robustness of the scheme. Thus, smaller values of ${\xi }_{ubf}$ provide more accuracy, while larger values increase the robustness of the scheme.

To maintain boundedness, the bounded central-differencing scheme turns into a first-order upwind scheme when the convection boundedness criterion is not satisfied, for example when $\xi <0\text{ or }1<\xi$ . The central-differencing scheme on the contrary, which is formally a second-order accurate scheme, does not do that. Thus, the bounded central-differencing scheme can be more dissipative than the central-differencing scheme—especially on coarser meshes.

Overall, the bounded central-differencing scheme provides a good compromise between accuracy (much improved, when compared with the second-order upwind scheme) and robustness (due to its warranted boundedness). It is the recommended scheme for LES of complex turbulent flows.

Hybrid MUSCL 3rd-Order/Central-Differencing

The scheme is valid for both steady and unsteady simulations, and has one model parameter ${\sigma }_{MUSCL3}$, which is used to control the numerical dissipation in the scheme. As with the bounded central-differencing scheme, this scheme uses a Normalized-Variable Diagram (NVD) value $\xi$ to ensure the boundedness of the scheme by switching to the first-order scheme in regions of non-smooth flows.

When smooth local flow conditions are detected, the scheme is constructed as a blend between a MUSCL 3rd-order upwind and a 3rd-order central-differencing reconstruction scheme.

The convective flux is computed as:

$${\left(\dot{m}\varphi \right)}_f=\{\begin{array}{cc}{\dot{m}\varphi }_{FOU}\hfill & for\xi <0or\xi >1\hfill \\ \dot{m}({\sigma }_{MUSCL3}{\varphi }_{MUSCL3}+(1-{\sigma }_{MUSCL3}){\varphi }_{CD3})\hfill & for0\le \xi \le 1\hfill \end{array}$$

(893)

The blending factor ${\sigma }_{MUSCL3}$ is user-controlled and must be decided based on the physical problem or model.

The MUSCL 3rd-order upwind reconstructed value ${\varphi }_{MUSCL3}$ is carefully limited at high speeds so as to not affect the formal order of accuracy while preventing spurious oscillations. The high speed limiting is based on WENO (Weighted Essentially Non-Oscillatory) principles and is only applied to the quadratic part of the face-value reconstruction. WENO-based averaging is computed based on three different stencils.

Note	The ${\varphi }_{MUSCL3}$ accuracy is reduced to second order in the regions next to the strong shocks.

The switch between the unlimited and the WENO-limited ${\varphi }_{MUSCL3}$ is done based on a Mach-number-based flux-limiter. For incompressible simulations, ${\varphi }_{MUSCL3}$ is unlimited (the flux limiter is 1), thus only relying on the use of the NVD value to ensure the boundedness of the scheme. Overall, the Hybrid MUSCL 3rd-order/CD scheme provides improved (reduced) dissipation when compared with both second-order and Bounded Central-Differencing (BCD) schemes. At the same time, it is robust (due to its boundedness) and capable of simulating steady and unsteady flows from incompressible to high-speed compressible regimes.

Hybrid Second-Order Upwind/Central-Differencing

The second-order upwind is the most accurate scheme for steady-state calculations, while the kinetic energy-preserving properties of the central-differencing scheme make it appropriate for large eddy simulation (LES). In this scheme, both approaches are blended as follows:

$${\left(\dot{m}\varphi \right)}_f=\{\begin{array}{c}{\dot{m}}_f\{{\sigma }_{HU}{\varphi }_{f,0}+\left(1-{\sigma }_{HU}\right)[f{\varphi }_{f,0}+\left(1-f\right){\varphi }_{f,1}]\}\text{for }{\dot{m}}_f\ge 0\\ {\dot{m}}_f\{{\sigma }_{HU}{\varphi }_{f,1}+\left(1-{\sigma }_{HU}\right)[f{\varphi }_{f,0}+\left(1-f\right){\varphi }_{f,1}]\}\text{for }{\dot{m}}_f<0\end{array}$$

(894)

where ${\sigma }_{HU}$ is a blending factor that is chosen as appropriate for the flow regime (see Eqn. (1450) and Eqn. (1306)). The face values ${\varphi }_{f,0}$ and ${\varphi }_{f,1}$ , are linearly interpolated from the cell values on either side of the face using the reconstruction gradients, as with the second-order upwind scheme.

Hybrid Second-Order Upwind/Bounded-Central

The following hybrid second-order upwind/bounded central scheme is the default for detached eddy simulations (DES) and Scale-Resolving Hybrid (SRH) simulations of complex turbulent flows:

$${\left(\dot{m}\varphi \right)}_f=\dot{m}({\sigma }_{HU}{\varphi }_{SOU}+(1-{\sigma }_{HU}\left){\varphi }_{BCD}\right)$$

(895)

where at face $f$ , the values of $\varphi$ are ${\varphi }_{SOU}$ for the second-order upwind scheme and ${\varphi }_{BCD}$ for the bounded central-differencing scheme. ${\sigma }_{HU}$ is a blending factor that is chosen as appropriate for the flow regime (see Eqn. (1450) for DES and Eqn. (1306) for SRH).

Diffusive Flux

The diffusive flux in Eqn. (879) through internal cell faces of a cell is discretized as:

where $\Gamma$ is the face diffusivity, $\nabla \varphi$ is the gradient of fluid property $\varphi$, and $\mathbf{\text{a}}$ is the surface area vector.

To obtain an accurate second-order expression for an interior face gradient that implicitly involves the cell values ${\varphi }_0$ and ${\varphi }_1$ , the following decomposition is used:

where:

The diffusion flux at an interior face can then be written as:

where ${\Gamma }_f$ is a harmonic average of the cell values.

A similar decomposition is used at a boundary face:

where:

The second and third terms in Eqn. (898) represent the secondary gradient (or cross-diffusion) contribution. They are essential for maintaining accuracy on non-orthogonal meshes.

The formulation that is presented above assumes that the centroids of cells 0 and 1 lie on opposing sides of the face. It is further assumed that their location is consistent with the convention that the face area vector points out of cell 0. To prevent non-physical solutions, take care to use meshes for which the angle between $\mathbf{\text{a}}$ and $\mathbf{\text{ds}}$ is not greater than 90 degrees.

To ensure that a valid mesh is being used, a diagnostic tool that is provided in Simcenter STAR-CCM+ allows this angle (termed skewness angle) to be computed in degrees and stored in adjacent cells. The value that is stored in each cell represents the largest skewness angle for each face of the cell.

As a further diagnostic tool that can be employed to check whether the secondary gradient contribution is destabilizing, these terms can be optionally omitted, in which case Eqn. (898) reduces to:

Similar to interior faces, the second and third terms in Eqn. (899) represent the boundary secondary gradient (or cross-diffusion) contribution.

As with the interior, these boundary secondary gradients can be optionally neglected as a further diagnostic tool, in which case Eqn. (899) reduces to:

Transient Term

For transient simulations, time is an additional coordinate. Generally, numerical procedures require that this coordinate is discretized in addition to a spatial discretization, that is, the total time interval is subdivided into time-steps. The solution of the governing equations is obtained at different time-levels whereby the solution at time $t$ requires the solutions from previous time-levels. Time integration schemes are distinguished between the number of time-levels they use for integration and on which time-level the fluxes and sources are integrated.

Implicit Time Integration

The Euler implicit scheme, a first-order temporal scheme, approximates the transient term in Eqn. (879) using the solution at the current time level, $n+1$ and the one from the previous time level, $n$ :

A basic second-order temporal discretization of the unsteady term uses the solution at the current time level, $n+1$ , as well as the solutions from the previous two time levels, $n$ and $n-1$ , in a Backward Differentiation Formula, BDF2.

BDF2 is:

On the first time-step of a second-order temporal simulation, a first-order discretization is used since only two time levels are available.

Second-order schemes using more time levels are linear combinations of BDFs.

The scheme for four time levels, BDF2Opt(4), is:

where BDF3 is:

The scheme uses the previous three time levels as well as the current one. It uses a first-order discretization on the first step and second-order and the second step, as time levels become available.

The scheme for five time levels, BDF2Opt(5), is:

where BDF4 is:

The scheme uses the previous four time levels and employs the first three discretizations on the first three steps, as time levels become available.

The formulas above use a constant time-step $\mathrm{\Delta }t$ throughout. But Simcenter STAR-CCM+ actually uses variable time-steps, to accommodate unevenly spaced time levels.

Gradients

In addition to variable values, variable gradients are required at cell centers and at cell-face centers for:

• construction of variable values at the cell faces
• secondary gradients calculation for diffusion terms
• pressure gradients calculation for pressure-velocity coupling
• strain-rate and rotation-rate calculations for turbulence models

Least Squares Method

The gradients in cell-0 are computed as:

$$\nabla \varphi =\left(\beta \right)\mathbf{\text{LSQ\_grad}}\left(\varphi \right)$$

(908)

where:

$$\mathbf{\text{LSQ\_grad}}\left(\varphi \right)=\sum _f{\mathbf{M}}^{-1}\cdot \left(w_f{\mathbf{\text{ds}}}_f\right)\delta {\varphi }_f=\sum _f{\mathbf{q}}_f\delta {\varphi }_f$$

(909)

where:

• ${\mathbf{\text{ds}}}_f={\mathbf{x}}_{c1}-{\mathbf{x}}_{c0}$ is the vector between the cell centers.
• $\delta {\varphi }_f={\varphi }_{c1}-{\varphi }_{c0}$ is the difference between the cell center values of the scalar $\varphi$ .
• The least squares tensor $\mathbf{M}$ is defined as:
  $$\mathbf{M}=\sum _f{w}_f{\mathbf{d}\mathbf{s}}_f\otimes {\mathbf{d}\mathbf{s}}_f$$
  with the weight:
  $$w_f=\frac{\left|A_f\right|}{\left|{\mathbf{d}\mathbf{s}}_f\right|V}$$
  where:
  • $\left|A_f\right|$ is the magnitude of the face area vector.
  • $\left|{\mathbf{d}\mathbf{s}}_f\right|$ is the length between the cell centers.
  • $V$ is the cell volume.

The scalar $\beta$ is computed as:

$$\beta =\text{min}(1,\frac{C_{\text{max}}^{\text{user}}}{{\text{max}}_{f,g}({\mathbf{x}}_{f0}\cdot {\mathbf{q}}_g)})$$

(910)

where:

• $C_{\text{max}}^{\text{user}}$ is the user-specified Maximum Reconstruction Coefficient (default value 1).
• ${\text{max}}_{f,g}$ is over all pairings $f,g$ of cell faces in the range of 1 to $N_{\text{faces}}$ .
• ${\mathbf{x}}_{f0}={\mathbf{x}}_f-{\mathbf{x}}_{c0}$ is the face-to-cell vector.
• ${\mathbf{q}}_f$ is defined in Eqn. (909).

Gradient Limiters

If unlimited gradients are used for reconstruction, the reconstructed face values can fall outside the range of cell values found in neighboring cells (connected through faces). For this reason, Simcenter STAR-CCM+ finds the minimum and maximum bounds of the neighboring cell values and uses these to limit the reconstruction gradients.

The following gradient limiters are available:

• Venkatakrishnan
• Min-Mod
• Modified Venkatakrishnan

The face value ( ${\varphi }_{f,0}$ ) reconstructed from the cell-0 value at any face centroid is given by:

where ${\mathbf{\text{s}}}_0={\mathbf{\text{x}}}_f-{\mathbf{\text{x}}}_0$ , ${\mathbf{\text{x}}}_f$ and ${\mathbf{\text{x}}}_0$ are the face and cell centroids, respectively, and $\nabla {\varphi }_{r,0}$ is the reconstruction gradient.

For each cell-0, a limited reconstruction gradient is required, such that the reconstructed face value does not exceed the maximum and minimum of the neighboring cell centroid values, including the value in cell-0. A scale factor $\alpha$ is defined that expresses the ratio of the limited and unlimited values, that is:

For each cell-0, the quantities are defined:

where ${\varphi }_{\text{neighbors}}$ represents the cell value in each neighbor that has a common face with cell-0.

These quantities can also be defined:

For each face f of cell-0, ${\mathrm{\Delta }}_f$ is defined as:

Now defining:

Venkatakrishnan

The Venkatakrishnan [292] limiter gives for the face:

$${\alpha }_f=\frac{2r_f+1}{r_f(2r_f+1)+1}$$

(915)

Min-Mod

The Min-Mod limiter gives for the face:

$${\alpha }_f=\text{min}(1,1/r_f)$$

(916)

Modified Venkatakrishnan

The Modified Venkatakrishnan limiter gives for the face:

$${\alpha }_f=\frac{r_f\text{(}2r_f+1)+1}{{r_f\text{(}r}_f(2r_f+1)+1)+1}$$

(917)

The Venkatakrishnan limiter is the default option. In certain cases, the Min-Mod and the modified Venkatakrishnan limiter can be less dissipative than the default option, particular in unsteady simulations for aeroacoustics or when using LES/DES for turbulence modeling.

The cell value of $\alpha$ is given by:

Total Variation Bounded Gradient

If gradients are excessively limited, convergence can slow or stall. This problem arises most often with the gradients of near-constant fields, or when the limiter cycles between 0 and 1 without settling on a convergence value.

To avoid this problem, Total Variation Bounded gradient limiting can be applied. Reconstructed values vary by an additional difference of

$$\delta =\psi \cdot \text{max}\left({\mathrm{\Delta }}_{\text{max}}-{\mathrm{\Delta }}_{\text{min}}\right)$$

(919)

where $\psi$ is a fraction between 0 and 1, and $\text{max}\left({\mathrm{\Delta }}_{\text{max}}-{\mathrm{\Delta }}_{\text{min}}\right)$ is the largest difference between local maximum and local minimum anywhere in the simulation.

The default value of $\psi$ is 0.05. Larger values of $\psi$ mean that gradients are limited less. This can improve accuracy, especially for smooth flow field gradient reconstruction. However, excessively large values can lead to loss of solver robustness and lower accuracy, by producing large over- or under-shoots at flow field discontinuities.

TVB Gradient Limiting is useful for high-fidelity simulations, such as aeroacoustics and turbulence simulations using Large Eddy Simulation (LES) or Detached Eddy Simulation (DES).

Boundary Conditions

The foregoing expressions for the evaluation of the convective and the diffusive fluxes above are valid for all interior cell faces. On faces that coincide with boundaries of the computational domain, boundary conditions are applied. The integrals over the boundary surface are expressed as a function of the known boundary data and cell values from the interior.

In the case of Neumann boundary conditions, the diffusive fluxes are calculated directly with the variable values at the boundary being obtained from the discretized gradient approximations.

Algebraic System of Equations

With $\mathrm{\Delta }{\varphi }_p={\varphi }_p^{k+1}-{\varphi }_p^k$, the algebraic system for the transported variable $\varphi$ is written in delta form:

where $\varphi$ is the transported variable at iteration $k+1$ (current iteration) or $k$ (previous iteration), respectively. The summation is over all the neighbors $n$ of cell $p$ . The right-hand side $r$ is the residual. The coefficients $a_p$ and $a_n$ are obtained directly from the discretized terms. $\omega$ is an under-relaxation factor.

The right-hand side:

is termed the residual, and represents the discretized form of the original equation (Eqn. (881)) at iteration k. By definition, then, the residual becomes zero when the discretized equation is satisfied exactly.

Due to the non-linear nature of the problem, an iterative solution is required. There are two levels of iteration; an outer iteration loop controlling the solution update and an inner loop governing the iterative solution of the linear system. Since the outer iterations are repeated multiple times, it is sufficient to solve the linear system only approximately at each outer iteration. The iterative solution of the linear system is accomplished using Algebraic Multigrid (AMG).