Constitutive Relations

Permittivity and Permeability

The constitutive relations between the electric field $E$ and the electric flux density $D$ , and between the magnetic field $H$ and the magnetic flux density $B$ can be generalized as:

where the permittivity $\epsilon$ describes the behavior of the material in response to an electric field, and the magnetic permeability $\mu$ describes the behavior of the material in response to a magnetic field. The inverse of the magnetic permeability is called the magnetic reluctivity, $\nu ={\mu }^{-1}$ .

For materials other than ferroelectrics and ferromagnets, Eqn. (4219) and Eqn. (4220) are approximately linear.

In general, $\epsilon$ and $\mu$ are represented by second-order tensors, which define linear transformations between the vectors $D$ - $E$ and $H$ - $B$ , respectively.

For example, for a 3D domain, Eqn. (4219) can be written in matrix form as:

or, for a 2D domain on the x-y plane, as:

For homogeneous materials, the components of $\epsilon$ and $\mu$ do not depend on the position inside the material. For inhomogeneous materials, the components are functions of the position.

In the special case of isotropic materials, $\epsilon$ and $\mu$ reduce to diagonal matrices, with diagonal components ${\epsilon }_{11}={\epsilon }_{22}={\epsilon }_{33}=\epsilon$ and ${\mu }_{11}={\mu }_{22}={\mu }_{33}=\mu$ , and can therefore be defined using scalar quantities. Specifically, $\epsilon$ can be defined with respect to the vacuum permittivity, ${\epsilon }_0=8.85\times {10}^{-12}[F/m]$ , as $\epsilon ={\epsilon }_r{\epsilon }_0$ , where ${\epsilon }_r$ is called the relative permittivity. $\mu$ can be defined with respect to the vacuum permeability, ${\mu }_0=4\pi \times {10}^{-7}\left[H/m\right]$ , as $\mu ={\mu }_r{\mu }_0$ , where ${\mu }_r$ is called the relative permeability. For paramagnetic materials, $\mu >{\mu }_0$ , whereas diamagnetic materials show $\mu <{\mu }_0$ .

Ferromagnetic materials show a nonlinear response to applied electromagnetic fields. For this type of materials, Eqn. (4220) becomes a nonlinear functional equation [848]:

In general, temperature changes can affect the magnetic permeability of ferromagnetic and paramagnetic materials. It is often convenient to express the dependence of $\mu$ on temperature through the magnetic susceptibility $\chi$ , which is defined as:

The dependence of $\chi$ on temperature can be approximated as:

where ${\chi }_{ref}\left(H\right)$ is the magnetic susceptibility at ambient temperature ( $T_{ref}=20C^{\circ }$ ) and $S\left(T\right)$ is the susceptibility temperature factor, with $S\left(T_{ref}\right)=1$ .

Ferromagnetic materials are often used in electric devices such as electric motors. The $B$ - $H$ curve, or hysteresis loop, of a ferromagnetic material has the following form:

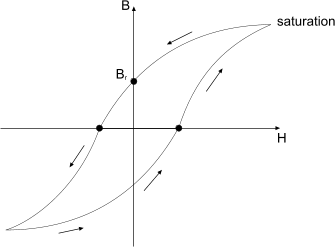
The image shows the magnetization process, where $B$ increases with $H$ until the material reaches saturation, and the demagnetization process, where $B$ decreases with $H$ until the material reaches (negative) saturation. Materials that exhibit a non-zero magnetic flux density, $B_r$ , when the applied magnetic field is zero, $H=0$ , are called permanent magnets. $B_r$ is called the remanent magnetic flux density.

For linear materials and soft materials which operate in the first quadrant of the $B\text{-}H$ characteristic, the energy density stored in the magnetic field is defined as:

For linear materials, the energy density is equal to the coenergy density, which is defined as:

Electrical Conductivity: Generalized Ohm's Law

The relationship between the electric current density $J$ and the electric field $E$ is described by the generalized Ohm's law:

where the electrical conductivity $\sigma$ describes the behavior of the material in response to electric currents. Like $\epsilon$ and $\mu$, $\sigma$ is generally defined by a second-order tensor, and reduces to a scalar in isotropic conducting materials.

Electrical Conductivity of Porous Materials

In Simcenter STAR-CCM+, you can model porous materials in one of two ways—using porous regions (legacy method), or fluid regions with the Porous Media model (recommended method).

For fluid regions that use the Porous Media model, you define the conductivity of the fluid and solid phases independently.

For porous regions, the electrical conductivity of the region can be modeled as a combination of the electrical conductivities of the fluid and solid components, using various methods:

$$\begin{array}{ll}\sigma =\frac{\chi }{\tau }{\sigma }_{\mathrm{fluid}}+\left(\frac{1-\chi }{\tau }\right){\sigma }_{\mathrm{solid}}& \mathrm{Volume\; Fraction\; Weighted\; Method}\\ \sigma ={\sigma }_{\mathrm{solid}}{(1-\chi )}^{\beta }& \mathrm{Bruggeman\; (solid)\; Method}\\ \sigma ={\sigma }_{\mathrm{fluid}}{\chi }^{\beta }& \mathrm{Bruggeman\; (fluid)\; Method}\end{array}$$

(4230)

where $\chi$ is the porosity of the material, $\tau$ is the tortuosity, ${\sigma }_{\mathrm{fluid}}$ is a scalar, ${\sigma }_{\mathrm{solid}}$ is a second-order tensor, and $\beta$ is the Bruggeman approximation exponent.

When calculating the effective electrical conductivity using the Bruggeman methods, Simcenter STAR-CCM+ automatically sets the tortuosity of the porous material to:

$$\begin{array}{c}\tau ={\chi }^{1-\beta }\end{array}$$

(4231)