Home
Theory
Simcenter STAR-CCM+ simulations are built on numerical algorithms that solve relevant laws of physics according to the conditions that the simulation defines. So that you can identify the physical laws, and understand the methods by which they are solved, Simcenter STAR-CCM+ comes with a Theory Guide.
Numerical Flow Solution
In the finite volume method, the solution domain is subdivided into a finite number of small control volumes, corresponding to the cells of a computational grid.
Finite Element Method for Viscoelastic Fluid Flow
In Simcenter STAR-CCM+, the numerical algorithm for capturing the complex flow field of non-Newtonian viscoelastic fluids is based on the finite element method. The discretization of a closed-form non-linear differential constitutive equation is described exemplarily by means of the Oldroyd-B model and can be readily extended to other differential constitutive equations.
Inverse Die Method
It is possible to start with the desired cross section of an extrudate and calculate back to the shape of the die needed to produce it.

Share

Link: copied

Breadcrumb: copied

Theory
Simcenter STAR-CCM+ simulations are built on numerical algorithms that solve relevant laws of physics according to the conditions that the simulation defines. So that you can identify the physical laws, and understand the methods by which they are solved, Simcenter STAR-CCM+ comes with a Theory Guide.
- Fundamental Equations
  Simcenter STAR-CCM+ models a range of physics phenomena including fluid mechanics, solid mechanics, heat transfer, electromagnetism, and chemical reactions. On a macroscopic scale, where the typical lengths are much greater than the inter-atomic distances, the discrete structure of matter can be neglected and materials can be modeled as continua. The mathematical models that describe the physics of continua are derived from fundamental laws that express conservation principles.
- Fluid Flow
  Simcenter STAR-CCM+ can simulate internal and external fluid flow across a wide range of flow regimes, and for a variety of fluid types. It solves the conservation equations for mass, momentum, and energy for general incompressible and compressible fluid flows.
- Numerical Flow Solution
  In the finite volume method, the solution domain is subdivided into a finite number of small control volumes, corresponding to the cells of a computational grid.
  - Finite Volume Discretization
    Generally, numerical methods, and this includes the finite-volume method, transform the mathematical model into a system of algebraic equations. This transformation involves discretizing the governing equations in space and time. The resulting linear equations are then solved with an algebraic multigrid solver.
  - Finite Element Method for Viscoelastic Fluid Flow
    In Simcenter STAR-CCM+, the numerical algorithm for capturing the complex flow field of non-Newtonian viscoelastic fluids is based on the finite element method. The discretization of a closed-form non-linear differential constitutive equation is described exemplarily by means of the Oldroyd-B model and can be readily extended to other differential constitutive equations.
    - Flow Boundary Conditions
      To complete the mathematical model, you specify conditions on the solution domain boundary.
    - Thermal Boundary Conditions
      In non-isothermal viscous flow, a thermal boundary condition must be specified on each boundary. The boundary condition is represented by the last term on the lefthand side of the [eqnlink]. On the velocity inlet, mass flow inlet, and stagnation inlet, a Dirichlet condition is imposed, that is, the static temperature at the boundary is specified. On the pressure outlet, a Neumann condition is imposed, that is, the viscous flow solver assumes zero flux at the boundary and the boundary term in [eqnlink] is dropped.
    - Viscous Multiphase Flow
      Multiphase flow and moving boundary problems are ubiquitous in industrial applications including chemical, cosmetics, food, printing, pharmaceutical and more recently microfluidics and lab on a chip applications. However, there are also many numerical complexities in simulation of multiphase ﬂows that are not present in single ﬂuid ﬂows. With the presence of multiple phases comes the requirement of tracking the interface between the phases. Moreover, in numerous applications, such as co-extrusion, film casting, calendaring, dip and roll coating, blends mixing and compounding, and so on, one or more phases involved in the process are complex fluids and thus it is necessary to have a multiphase solver capable of handling the complex rheology of processing fluids. In Simcenter STAR-CCM+, the Conservative Level-Set method is used for this purpose.
    - Conservative Level Set
      For cases involving multiple phases of viscous fluid, the different phases are tracked by a set of functions of the form $φ_{i} (x, t)$ . The function $φ_{i} (x, t)$ denotes the regions of the domain occupied by phase $i$ at an arbitrary spatial point $x$ and time $t$ .
    - Partial Fill Method
      The partial fill method handles incompressible viscous liquids that only partially fill a volume, the rest of the volume being filled with air or another gas. The principal use is in modeling the filling stage of injection molding.
    - Inverse Die Method
      It is possible to start with the desired cross section of an extrudate and calculate back to the shape of the die needed to produce it.
    - Curing Method
      The curing method applies to viscous flows that change physical and chemical properties during the course of the simulation.
    - Linear System of Equations
      A Newton-Raphson iteration algorithm was used to capture the solution of non-linear algebraic equations.
  - Smoothed-Particle Hydrodynamics (SPH) Method for Multiphase Flow
    Smoothed-Particle Hydrodynamics (SPH) is a mesh-free Lagrangian numerical method that overcomes the volume mesh related limitations of the finite volume methods while still being based on the Navier-Stokes equations. This method is particularly suited for applications with highly dynamic free surface flows and complex moving geometries.
  - Numerical Flow Solution Bibliography
- Turbulence
- Transition
  The term transition refers to the phenomenon of laminar to turbulence transition in boundary layers. A transition model in combination with a turbulence model predicts the onset of transition in a turbulent boundary layer.
- Wall Treatment
  Walls are a source of vorticity in most flow problems of practical importance. Therefore, an accurate prediction of the flow across the wall boundary layer is essential.
- Wall Distance
  Wall distance is a parameter that represents the distance from a cell centroid to the nearest wall face with a non-slip boundary condition. Various physical models require this parameter to account for near-wall effects.
- Heat Transfer
  Heat transfer is the exchange of thermal energy between media at different temperatures. Heat transfers from locations of high temperature to locations of low temperature in order to reach an equilibrium state. The three main mechanisms of heat transfer are: conduction, convection, and radiation.
- Porous Media
  Porous media are continua that contain both fluid and fine-scale solid structures, for example: packed-bed chemical reactors, filters, radiators, honeycomb structures, or fibrous materials. The solid geometrical structures are too fine to be individually meshed and fully resolved by a computational grid.
- Species and Passive Scalars
  Simcenter STAR-CCM+ models the transport, the mixing, and the chemical reactions of multi-component liquids or multi-component gases by solving conservation equations for scalar variables that represent the mass fraction of each species in the mixture. This conservation equation allows for convection, diffusion, and optional source effects, and is solved in addition to the global mass continuity equation.
- Multiphase—Eulerian Approach
  Multiphase flows, where several fluids flow in the domain of interest, play an important role in variety of industrial applications. In general, we associate phases with gases, liquids or solids and as such some simple examples of multiphase flows are: air bubbles rising in a glass of water, sand particles carried by wind, rain drops in air. The definition of phase can be generalized and applied to other fluid characteristics such as size, shape, density, and temperature.
- Multiphase—Lagrangian Approach
  Multiphase flows are found in a wide variety of industrial processes, some examples of which are internal combustion engines, liquid, or solid fueled combustors, spray driers, cyclone dust separators, and chemical reactors. Multiphase in this context refers to one thermodynamic phase, be it a solid, a liquid, or a gas, interacting with another distinct phase.
- Reacting Flow
  In reacting flows, chemical species mix with each other and react when conditions allow. To model these flows, Simcenter STAR-CCM+ couples species and energy transport equations with the chemistry solvers that compute the source terms.
- Internal Combustion Engines
  Numerical modeling of internal combustion engines plays an increasingly important role in improving engine design. CFD simulation of such engines can give a comprehensive insight into the wide-ranging physics of the device, such as turbulent mixing between fuel and air, the ignition, and combustion chemistry.
- Electrochemistry
  Electrochemistry is the discipline investigating relationships between electrical currents and chemical composition change in general.
- Plasma
  Plasma is a state of matter similar to a gas that is composed partially or completely of charged particles such as ions and electrons which are not bound to each other.
- Electromagnetism
  Many engineering applications, such as electric motors, electric switches, and transformers, involve electromagnetic phenomena. Electromagnetic phenomena can be modeled based on the classical theory of Electromagnetism, which describes the interaction between electrically charged particles in terms of electric fields, magnetic fields, and their mutual interaction.
- Batteries
- Solid Mechanics
  Solid Mechanics describes the behavior of a solid continuum in response to applied loads. Applied loads include body forces, surface loads, point forces, or thermal loads that result from changes in the solid temperature. Applied loads induce a stress field in the structure and can cause displacement of the structure—from an initial undeformed configuration to a deformed configuration.
- Aeroacoustics
  Computational aeroacoustics (CAA) is a branch of multiphysics modeling and simulation that involves identifying noise sources that are induced by fluid flow and propagation of the sound waves then generated.
- Finite Element Method
  The Finite Element method is a powerful tool for finding approximate solutions to continuous problems. The methodology is similar to other numerical techniques that approximate continuous partial differential equations with discrete algebraic equations.
- Mesh Motion
  In transient simulations, mesh motion is a numerical technique that allows you to update the position of the computational domain while the solvers run.
- 6-DOF Rigid Body Motion
  Simcenter STAR-CCM+ allows you to model the motion of a rigid body in response to applied forces and moments. In a rigid body, the relative distance between internal points does not change. Therefore, it is sufficient to solve the equations of motion for the center of mass of the body.
- Rotating Flow
  Rotating flow usually occurs in rotating machinery such as pumps, propellers, fans, wind turbines, and so on.
- Harmonic Balance
  Harmonic Balance equations describe periodic unsteady flows where the unsteady frequencies are known beforehand. They are suited to modeling periodically repeating flow fields that typically occur in turbomachinery such as compressors, turbines, and fans.
- Adjoint
  The adjoint method is an efficient means to predict the influence of many input parameters on some engineering quantities of interest in a simulation.
- Design Manager
  Design Manager provides an automated approach within Simcenter STAR-CCM+ to run design exploration studies. Design exploration covers both performance assessment and optimization.
- Scalars, Vectors, and Tensors
  Most physical quantities in Simcenter STAR-CCM+ are either scalars, vectors, or 2nd-order tensors.
- Solution Data Interpolation
  Many operations require interpolation of solution data between different sets of mesh points. For example, remeshing operations require interpolation of existing solution data onto a new mesh. Data interpolation also occurs at the interface between regions, where contacting boundaries exchange data. Additionally, configurable data mappers allow you to interpolate field functions and tabular data to specified meshes.
- Idealizations
  In many simulations, it is common practice to reduce the size of the computational domain using planes of symmetry, axes of rotation, periodicity, or by reducing the 3D domain to a 2D domain. However, when you calculate physical quantities using reports you generally want to account for the whole domain. You can obtain report values for the full model using idealizations.

Inverse Die Method

It is possible to start with the desired cross section of an extrudate and calculate back to the shape of the die needed to produce it.

In the direct extrusion problem, the die surfaces are all stationary, but free stream surfaces must move in order to satisfy the dynamic and kinematic boundary conditions. In particular, the kinematic boundary condition on a free stream can be written as:

v \cdot n = 0

where $v$ is the velocity vector field and $n$ is the unit normal on the boundary. The above equation requires only one boundary condition along a line that crosses every velocity streamline. For direct extrusion, this condition would be imposed at the die lip. Alternatively, the boundary condition can be adopted at the end of the extrudate section (exit) and hence in this case the extrudate inlet (die lip) must be adapted. This can be achieved by allowing the die to be deformed.

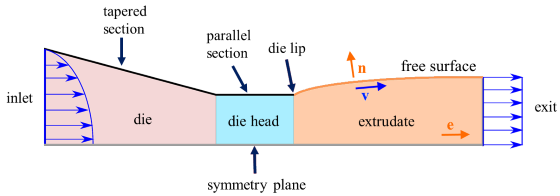
As shown in the figure above, this die adaptation is usually made in two parts: a linear section followed by a short parallel section. Both sections are particular cases of a linear adaptation in the extrusion direction $e$ .

A local principle from elementary differential geometry expresses the linearity in the extrusion direction $e$ :

\nabla\cdot (e \cdot \nabla d) = 0

where $d$ is the displacement vector. The variational form of the above equation is multiplied by the weight function $\tilde{d}$ and then integrated by parts. A stiffness coefficient $k$ is then introduced to give:

\int_{Ω} k (e \cdot \nabla \tilde{d}) \cdot (e \cdot \nabla d) d Ω = 0, \forall \tilde{d} \in {(H_{0}^{1} (Ω))}^{3}

where $H_{0}^{1} (Ω)$ denotes the Sobolev space consisting of square integrable functions for which the first derivatives are also square integrable, with the magnitude zero at the boundaries with essential (Dirichlet) boundary conditions. However, applying the above linearity requirement only in the normal direction (to the die boundary) yields:

\int_{Ω} k (e \cdot \nabla \tilde{d} \cdot n) \cdot (e \cdot \nabla d \cdot n) d Ω = 0, \forall \tilde{d} \in {(H_{0}^{1} (Ω))}^{3}

The distinction between tapered and parallel sections is made by a distinction in the stiffness $k$ (greater value for the parallel section than for the tapered section).

Finally, note that the inverse die design can only be used in steady state condition.