Collision and Coalescence

Simcenter STAR-CCM+ uses a host cell approach to detect collisions. Two parcels can collide only if they are in the same cell. Simcenter STAR-CCM+ uses the faster of the following collision algorithms to detect collisions in any particular cell. The following algorithms are available:

the NTC (No Time Counter) collision detection algorithm [699]
the O’Rourke algorithm [679]

After a collision is detected between two droplets, different collision outcomes are possible: bounce, coalescence, reflexive separation, and stretching separation (grazing collision) [659]:

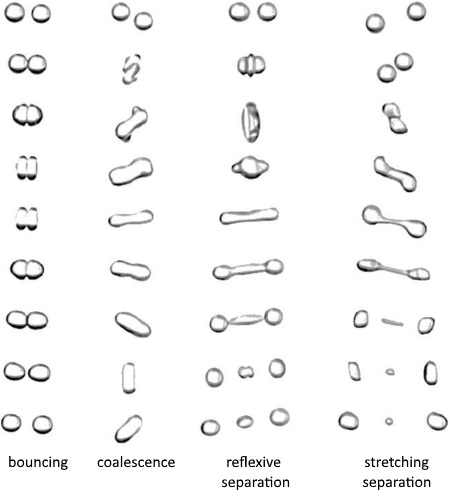
This implementation ignores the formation of satellite droplets which may occur at high collision Weber numbers.

Collision outcomes are described by three non-dimensional parameters:

The collision Weber number ${We}_{coll}$ is:
Figure 1. EQUATION_DISPLAY

${We}_{coll} = \frac{ρ_{l} {(v_{1, 2})}^{2} (r_{1} + r_{2})}{2 σ}$

(3142)

where $σ = \frac{1}{2} (σ_{1} + σ_{2})$ is the average surface tension of droplets 1 and 2 and $ρ_{l} = \frac{1}{2} (ρ_{1} + ρ_{2})$ is the average density. The relative velocity $v_{1, 2}$ is:
Figure 2. EQUATION_DISPLAY

$v_{1, 2} = | v_{1} - v_{2} |$

(3143)

where $v_{1}$ and $v_{2}$ are the velocities of the colliding droplets, and $r_{1}$ and $r_{2}$ are their corresponding radii.
The collision Weber number can also be defined based on the diameter of the smaller droplet $d_{s}$ , which in relation to ${We}_{coll}$ is given as:
Figure 3. EQUATION_DISPLAY

${We}_{d} = \frac{ρ_{l} {(v_{1, 2})}^{2} d_{s}}{σ} = \frac{4 Δ}{(1 + Δ)} {We}_{c o l l}$

(3144)
The impact parameter $B$ is:
Figure 4. EQUATION_DISPLAY

$B = \frac{b}{r_{1} + r_{2}}$

(3145)

where $b$ is calculated by taking the distance from the center of one droplet to the relative velocity vector that is placed on the center of the other droplet. When $B = 0$ , the collision is head-on. When $B = 1$ , the droplets barely graze each other.
The droplet size ratio $γ$ is:
Figure 5. EQUATION_DISPLAY

$γ = \frac{r_{2}}{r_{1}}, r_{2} > r_{1}$

(3146)
An additional size ratio parameter commonly used in literature is $Δ = \frac{1}{γ}, 0 < Δ < 1$ .
The collision Ohnesorge number $O h$ is defined as:
$O h = \frac{μ}{\sqrt{ρ σ d_{s}}}$
where $μ$ is the averaged dynamic viscosity of the colliding droplets.

The outcome of a collision can be represented with a collision outcome map based on the impact parameter $B$ and the collision Weber number $We$ . Droplets bounce off each other (simple bounce or reflexive separation), coalesce, or graze each other (stretching separation) according to their position on the collision outcome map. The general shape of the curves can shift with differing size ratio parameter as well as other physical properties such as droplet viscosity.

Three collision outcome maps are implemented in Simcenter STAR-CCM+ . The O'Rourke map ([678], [671]), the Ashgriz map ([645]), and the Composite map.

The O'Rourke and Ashgiz maps plot the collision efficiency $E$ versus the collision Weber number ${We}_{coll}$ which is calculated by Eqn. (3142) for each pair of interacting droplets based on an averaged droplet diameter. The collision efficiency $E$ is defined as the probability of obtaining a given outcome ( $E = B \cdot B$ ). The effect of energy loss due to viscous dissipation is not included in either of these two maps.

O'Rourke Map: The O'Rourke Map accounts for bounce, coalescence, and stretching/grazing separation modes.
Ashgriz Map: The Ashgriz map accounts for coalescence, reflexive separation, and stretching/grazing separation modes.

The boundaries of the coalescence area are described by the curves $E_{coal}$ and $E_{bounce}$ or $E_{graze}$ and $E_{reflex}$ .

For each $E$ curve:

Figure 6. EQUATION_DISPLAY

E_{i} = min [1.0, A {(\frac{We - {We}_{c}}{g (γ)})}^{a}]

(3147)

where $A$ , $a$ , and ${We}_{c}$ are empirical constants that are used to fit the $E$ curve to the data.

The default values for these constants are:


	O'Rourke		Ashgriz
	$E_{coal}$	$E_{bounce}$	$E_{graze}$	$E_{reflex}$
$a$	-1.0	$\frac{1}{3}$	$- \frac{2}{3}$	$\frac{2}{3}$
$A$	1.0	1.0	1.0	0.005
${We}_{c}$	0.0	0.0	0.0	20

The droplet diameter ratio correction is defined as:

Figure 7. EQUATION_DISPLAY

g (γ) = a_{3} γ^{3} + a_{2} γ^{2} + a_{1} γ + a_{0}

(3148)

where $γ$ is the droplet size ratio. The default values for the constants are:

$a_{3} = 2.4$
$a_{2} = - 5.76$
$a_{1} = 6.48$
$a_{0} = 0$

Using the default values for O'Rourke listed in the previous table, Eqn. (3147) for $E_{coal}$ and $E_{bounce}$ reduce to these formulations for collision and coalescence:

Figure 8. EQUATION_DISPLAY

E_{coal} = min [1.0, \frac{g (γ)}{W e}]

(3149)

Figure 9. EQUATION_DISPLAY

E_{bounce} = min [1.0, {(\frac{W e}{g (γ)})}^{\frac{1}{3}}]

(3150)

The O'Rourke algorithm for overall collision dynamics is described in the following flowchart [671]:

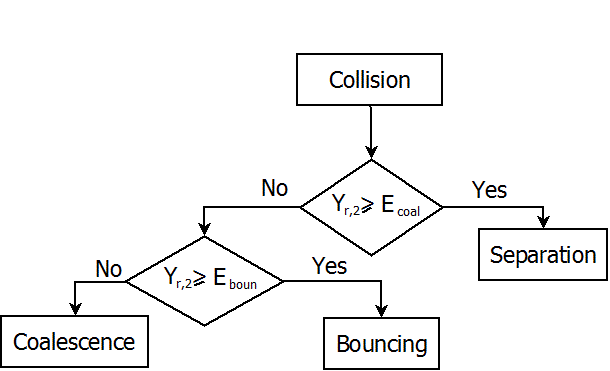
$Y_{r, 2}$ is a random number in the range [0,1].

For both O'Rourke and Ashgriz methods, if coalescence occurs, the number of coalescences $m$ that each droplet undergoes is determined by finding the value of $m$ for which

Figure 10. EQUATION_DISPLAY

\sum_{n = 0}^{m - 1} P_{n} < Y_{r, 2} < \sum_{n = 0}^{m} P_{n}

(3151)

where $P_{n}$ is the probability of $n$ collisions given by Eqn. (3176).

When coalescence occurs, the number of droplets from the less populous parcel is subtracted from the more populous parcel. If the outcome is grazing collision or bounce, only one collision is calculated per droplet. The post-collision velocity, temperature, and mass of the droplets are calculated based on the conservation of mass, momentum, and energy.

Composite Map

The Composite map provides models for the three boundary curves. The Sommerfeld model for bounce, the Suo-Jia model for stretching separation, and the Ashgriz model for reflexive separation.

Sommerfeld

This model was based on the approach of Hu et al. [664], where the effect of viscous dissipation in the energy balance is accounted for in the critical collision Weber number.

Figure 11. EQUATION_DISPLAY

{We}_{d} = \frac{g (Δ) (Φ - 3)}{(1 - B^{2}) (1 - β)}

(3152)

where:

$g (Δ) = \frac{4 (1 + Δ^{2}) (1 + Δ^{3})}{Δ^{2}}$
$β$ is the energy dissipation factor
$Φ$ is a shape factor related to the degree of deformation of the droplets during the colliding process.

The Sommerfeld ([709], [705]) approach automatically adapts $β$ and $Φ$ by fitting the available data with varying viscosity, limited by $O h < 0.5$ (for pure liquids) and $O h < 0.4$ (for solutions). The parameters $β$ and $Φ$ are assumed to be linear function of $B$ .

Figure 12. EQUATION_DISPLAY

Φ (B) = - k_{Φ} O h + Φ_{i n i t} O h

(3153)

Figure 13. EQUATION_DISPLAY

β (B) = (1 - β_{i n i t}) O h + β_{i n i t} O h

(3154)

Figure 14. EQUATION_DISPLAY

\begin{matrix} \begin{matrix} k_{Φ} = \max (k_{3} {O h}^{3} + k_{2} {O h}^{2} + k_{1} O h + k_{0}, k_{l}) \\ Φ_{i n i t} = \max (Φ_{3} {O h}^{3} + Φ_{2} {O h}^{2} + Φ_{1} O h + Φ_{0}, Φ_{l}) \\ β_{i n i t} = \min (β_{3} {O h}^{3} + β_{2} {O h}^{2} + β_{1} O h + β_{0}, β_{l}) \end{matrix} \end{matrix}

(3155)

The default values for these constants are:


Constants	$k_{0}$	$k_{1}$	$k_{2}$	$k_{3}$	$k_{l}$
Pure Liquid	0.82	-4.03	10.93	-9.6	0.31
Solution	0.725	-10.2	52.5	-87.7	0.0834


Constants	$Φ_{0}$	$Φ_{1}$	$Φ_{2}$	$Φ_{3}$	$Φ_{l}$
Pure Liquid	3.9	-4.32	12.4	-11.7	3.4
Solution	3.76	-6.05	18.31	-18.25	3.1


$β_{0}$	$β_{1}$	$β_{2}$	$β_{3}$	$β_{l}$
0.07	5.24	-19.6	22.6	0.5

For the case of head-on collision (B = 0), the critical Weber number is ${We}_{d} = \frac{g (Δ) (Φ - 3)}{(1 - β)}$ .

Suo-Jia

The Suo and Jia ([710]) model for stretching separation includes only dimensionless parameters as given below:

Figure 15. EQUATION_DISPLAY

\sqrt{{We}_{d}} = \frac{1}{B} (a + \frac{h}{d_{s}} O h)

(3156)

where a is a function of the Ohnesorge number and the droplet size ratio, given as:

Figure 16. EQUATION_DISPLAY

a = (a_{0} - a_{1} Δ) O h + a_{2}

(3157)

The default values for the constants are:

$a_{2} = 2.58$
$a_{1} = 180$
$a_{0} = 183$

This correlation is valid for :

$\begin{matrix} \begin{matrix} 1 m P a s < μ < 47.2 m P a s \end{matrix} & f o r & Δ = 1 \\ 1 m P a s < μ < 1.2 m P a s & f o r & Δ < 1 \end{matrix}$

Ashgriz: The Ashgriz method separates the reflexive separation and coalescence modes for the critical Weber number.
Figure 17. EQUATION_DISPLAY

${We}_{d} = \frac{f (Δ)}{Δ^{6} η_{s} + η_{l}}$

(3158)
where:
Figure 18. EQUATION_DISPLAY

$\begin{matrix} η_{s} = 2 {(1 - ξ)}^{2} {(1 - ξ^{2})}^{\frac{1}{2}} - 1 \\ η_{l} = 2 {(Δ - ξ)}^{2} {(Δ^{2} - ξ^{2})}^{\frac{1}{2}} - Δ^{3} \end{matrix}$

(3159)
and $ξ = \frac{1}{2} B (1 + Δ)$
Figure 19. EQUATION_DISPLAY

$f (Δ) = 3 Δ {(1 + Δ^{3})}^{2} [7 {(1 + Δ^{3})}^{\frac{2}{3}} - 4 (1 + Δ^{2})]$

(3160)
For the case of head-on collision (B = 0), the critical Weber number is ${We}_{d} = \frac{f (Δ)}{Δ^{3} (1 + Δ^{3})}$ . For a head-on collision of equal-sized droplets ${We}_{d} = 18.67$ . This number increases with increasing droplet size disparity.

Grazing Collisions

The threshold condition for grazing separation is $Y_{r, 2} \geq E_{c o a l}$ for the O'Rourke method or $Y_{r, 2} \geq E_{g r a z e}$ for Ashgriz. On the assumption that droplets retain their original size in grazing collisions, the new velocities of the droplets are:

Figure 20. EQUATION_DISPLAY

\begin{matrix} v_{1}^{n e w} = \frac{1}{m_{1} + m_{2}} [m_{1} v_{1} + m_{2} v_{2} + m_{2} (v_{1} - v_{2}) \frac{Y_{r, 2}^{\frac{1}{2}} - E_{c o a l}^{\frac{1}{2}}}{1 - E_{c o a l}^{\frac{1}{2}}}] \\ v_{2}^{n e w} = \frac{1}{m_{1} + m_{2}} [m_{1} v_{1} + m_{2} v_{2} + m_{1} (v_{2} - v_{1}) \frac{Y_{r, 2}^{\frac{1}{2}} - E_{c o a l}^{\frac{1}{2}}}{1 - E_{c o a l}^{\frac{1}{2}}}] \end{matrix}

(3161)

where $m_{1}$ and $m_{2}$ are the masses of the more and less populous parcels respectively.

Satellite droplet formation is ignored in grazing collisions. One collision is calculated for each droplet. The velocity of the more populous parcel is updated to account for droplets that did not take part in the collision:

Figure 21. EQUATION_DISPLAY

\begin{array}{l} v_{1}^{f i n a l} = \frac{N_{2} v_{1}^{n e w} + (N_{1} - N_{2}) v_{1}}{N_{1}} \\ v_{2}^{f i n a l} = v_{2}^{n e w} \end{array}

(3162)

where $N_{1}$ and $N_{2}$ are the numbers of particles in the more and less populous parcels respectively.

Bouncing

The threshold condition for bouncing is $Y_{r, 2} \geq E_{b o u n}$ .

The new velocities of the bouncing particles are given by:

Figure 22. EQUATION_DISPLAY

\begin{matrix} v_{1}^{n e w} = \frac{1}{m_{1} + m_{2}} [m_{1} v_{1} + m_{2} v_{2} - m_{2} (v_{1} - v_{2}) \frac{Y_{r, 2}^{\frac{1}{2}} - E_{b o u n ce}^{\frac{1}{2}}}{1 - E_{b o u n ce}^{\frac{1}{2}}}] \\ v_{2}^{n e w} = \frac{1}{m_{1} + m_{2}} [m_{1} v_{1} + m_{2} v_{2} - m_{1} (v_{2} - v_{1}) \frac{Y_{r, 2}^{\frac{1}{2}} - E_{b o u n ce}^{\frac{1}{2}}}{1 - E_{b o u n ce}^{\frac{1}{2}}}] \end{matrix}

(3163)

As in the case of a grazing collision, the velocity of the more populous parcel is updated to account for droplets that did not take part in the collision.

Reflexive Separation

The threshold condition for reflexive separation is $Y_{r, 2} < E_{reflex}$ .

The new velocities of the droplets after reflexive separation are:

Figure 23. EQUATION_DISPLAY

v_{1}^{new} = \frac{1}{m_{1} + m_{2}} [m_{1} v_{1} + m_{2} v_{2} - m_{2} (v_{1} - v_{2}) \sqrt{1 - \frac{{We}_{reflex}}{We}}]

(3164)

Figure 24. EQUATION_DISPLAY

v_{2}^{new} = \frac{1}{m_{1} + m_{2}} [m_{1} v_{1} + m_{2} v_{2} - m_{1} (v_{2} - v_{1}) \sqrt{1 - \frac{{We}_{reflex}}{We}}]

(3165)

${We}_{reflex}$ is defined from the equation for the $E_{reflex}$ curve ( $Y_{r, 2} = E_{reflex}$ ):

Figure 25. EQUATION_DISPLAY

Y_{r, 2} = E_{reflex} = min [1.0, A {(\frac{{We}_{reflex} - {We}_{c}}{g (γ)})}^{a}]

(3166)

NTC Detection Algorithm

The NTC model uses two algorithms for detection parcel collisions. By default it uses the NTC detection algorithm, but when parcel density becomes high, it switches to the O'Rourke detection algorithm.

The NTC algorithm is more efficient for a large number of parcels in sparse sprays. NTC considers only a sample of collision pairs but scales up the collision probability so that each pair is more likely to be selected. On average, the result is the same as if the full distribution was modeled directly.

If a cell contains $N$ droplets, the expected number of collisions in the cell over a time interval is given by summing the probability of all possible collisions:

Figure 26. EQUATION_DISPLAY

M_{coll} = \frac{1}{2} \sum_{i = 1}^{N_{p}} q_{i} \sum_{j = 1}^{N_{p}} q_{j} \frac{v_{i, j} σ_{i, j} Δ t}{V}

(3167)

where:

$v_{i, j}$ is the relative velocity between two colliding parcels
$σ_{i, j}$ is the collision cross section of the two droplets defined as
Figure 27. EQUATION_DISPLAY

$σ_{i, j} = π {(r_{i} + r_{j})}^{2}$

(3168)
$Δ t$ is the time-step size
$V$ is the cell volume
$N_{p}$ is the number of parcels in a cell
$q_{i}$ is the number of droplets in parcel $i$ .

The factor of one-half is a result of symmetry. This summation can be modified by pulling a constant factor outside:

Figure 28. EQUATION_DISPLAY

M_{coll} = \frac{{(q v σ)}_{max} Δ t}{2 V} \sum_{i = 1}^{N_{p}} q_{i} \sum_{j = 1}^{N_{p}} \frac{q_{j} v_{i, j} σ_{i, j}}{{(q v σ)}_{max}}

(3169)

The value of ${(q v σ)}_{max}$ is used for scaling the selection probability of a collision. The chosen value is sufficiently large so that the following restriction holds

Figure 29. EQUATION_DISPLAY

\frac{q_{j} v_{i, j} σ_{i, j}}{{(q v σ)}_{max}} < 1

(3170)

It is assumed that a representative subsample of parcels may be randomly selected from the set of parcels in the cell. This statistical approximation allows a constant multiplier to reduce the limits of summation as follows:

Figure 30. EQUATION_DISPLAY

M_{coll} = \sum_{i = 1}^{\sqrt{M_{cand}}} q_{i} \sum_{j = 1}^{\sqrt{M_{cand}}} \frac{q_{j} v_{i, j} σ_{i, j}}{{(q v σ)}_{max}}

(3171)

where

Figure 31. EQUATION_DISPLAY

M_{cand} = \frac{{N_{p}}^{2} {(q v σ)}_{\max} Δ t}{2 V}

(3172)

The overall cost is proportional to the product of the limits of the summation, namely $M_{cand}$ . The value of $M_{cand}$ is linearly proportional to $N_{p}$ , because $q$ goes as $1 / N_{p}$ . The double summation is evaluated using an acceptance-rejection scheme. The number of candidate pairs ( $M_{cand}$ ) is selected randomly from the cell population.

After a pair has been selected, a random number from a uniform distribution (from 0 to 1) is used to determine if the candidate pair actually collides. A new random number is chosen for every pair, even for pairs within the same cell. A collision takes place between parcels $i$ and $j$ if the deviate $r$ satisfies the inequality

Figure 32. EQUATION_DISPLAY

r < \frac{q_{g} v_{i, j} σ_{i, j}}{{(q v σ)}_{max}}

(3173)

The variable $q_{g}$ represents the greater number of droplets between $q_{i}$ and $q_{j}$ . If the collision is accepted, then $q_{l}$ , the lesser number of droplets, actually participates in the collision. This distinction is important in the case of droplet coalescence, where one parcel of droplets absorbs the other. Whenever employed for a given cell, the NTC algorithm is linearly proportional to $N_{p}$ .

If the spray is so dense that $M_{cand} > {N_{p}}^{2} / 2$ , then direct calculation of collisions using the O’Rourke approach is more efficient than the NTC algorithm for this cell. Simcenter STAR-CCM+ then switches to the O’Rourke algorithm automatically.

O’Rourke Detection Algorithm

The O’Rourke collision detection algorithm is a direct technique because it considers all possible collision partners. Compare to the NTC detection model, which samples collision pairs and scales the collision probability according to the results.

The probability of any droplet colliding with any other droplet is given by

Figure 33. EQUATION_DISPLAY

p_{i, j} = \frac{v_{i, j} σ_{i, j} Δ t}{V}

(3174)

The mean expected number of collisions between a droplet in parcel $i$ and the droplets in parcel $j$ is given by

Figure 34. EQUATION_DISPLAY

\bar{μ} = q_{j} \frac{v_{i, j} σ_{i, j} Δ t}{V}

(3175)

The number of collisions is determined by sampling from a Poisson distribution with a mean of $\bar{μ}$ :

Figure 35. EQUATION_DISPLAY

P_{n} = \frac{\bar{μ}}{n!} e^{- \bar{μ}}

(3176)

Eqn. (3176) gives the probability of $n$ collisions. $P_{0}$ gives the probability of zero collisions. Thus, whenever employed for a given cell, the O’Rourke approach is proportional to ${N_{p}}^{2}$ .