Multilayer Film Casting

Film casting is a process in which a thin film is extruded from a slot die and then, while molten, stretched with a cold metallic roller. The film can consist of one or several layers. The main purpose of the stretching in the casting process is to reduce the thickness of the film to the desired value. The thickness of the film is much smaller than the other two dimensions, so to analyze this problem a thin film model is required.

The following diagram shows a multilayer film casting process schematically:

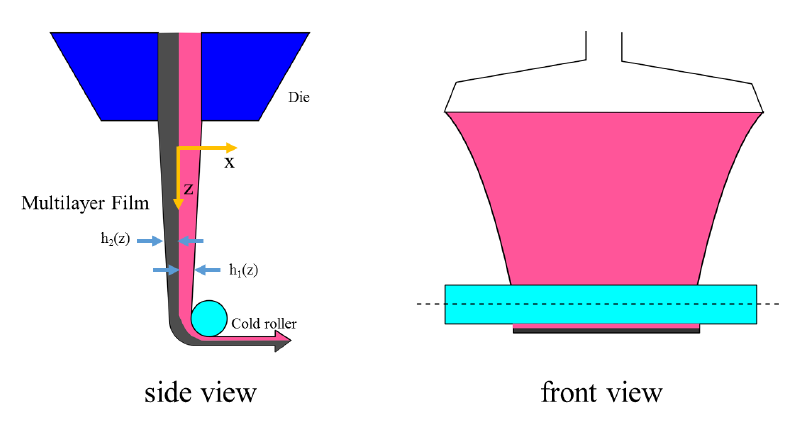
The thickness of layer $i$ is denoted by $h_{i}, i=1, \dots N$ in the $z$ direction, where $N$ denotes the number of layers. The thickness of the film is negligible compared to the length and width, that is $h_{i} ≪ l \sim w$ . Therefore, to obtain the governing equations describing the dynamics of a thin film with multiple incompressible viscoelastic fluids in an unsteady state, it is legitimate to assume the variations of velocity components in $x$ and $y$ in the thickness direction $z$ can be neglected and $v_{z}$ is only a function of $z$ [233]:

\begin{array}{l} v_{x} = v_{x} (x, y, t) \\ \begin{matrix} v_{y} = v_{y} (x, y, t) \\ v_{z} = v_{z} (z, t) \end{matrix} \end{array}

Using the incompressibility condition of the fluid, it can be shown that:

Figure 1. EQUATION_DISPLAY

\frac{d v_{z}}{d z} = - \nabla_{s} \cdot v

(745)

where $\nabla_{s} = (I - e_{z} e_{z}) \cdot \nabla$ . $\nabla_{s}$ is the surface gradient operator, $e_{z}$ is the unit normal vector in the $z$ direction, and $I$ is the identity tensor.

Imposing a force balance for a thin film with thickness:

Figure 2. EQUATION_DISPLAY

h = \sum_{i = 1}^{N} h_{i}

(746)

in the $x$ and $y$ directions according to the film membrane momentum equilibrium, adopting stress free and iso-strain assumptions for the $z$ direction, and ignoring interfacial tension at the boundaries (i.e. high capillary numbers), the momentum equation for the film can be written as:

Figure 3. EQUATION_DISPLAY

\sum_{i = 1}^{N} ρ_{i} h_{i} [\frac{\partial v}{\partial t} + (v \cdot \nabla_{s} v)] = \sum_{i = 1}^{N} \nabla_{s} \cdot [h_{i} (- T_{i}^{z z} I + T_{i})]

(747)

where:

$ρ_{i}$ is the fluid density of layer $i$ .
$p_{i}$ is the pressure.
$τ_{i}$ is the hydrodynamic stress tensor in the $i$ th layer.

The total hydrodynamic stress tensor $T_{i}$ can be defined as $T_{i} = 2 μ_{i} D + T_{i}^{p}$ , where:

$μ_{i}$ is the solvent viscosity associated with the $i$ th layer.
$D$ is the strain rate tensor.
$T_{i}^{p}$ is the viscoelastic contribution to the stress tensor associated with the $i$ th layer.

The local mass conservation of the thin film must be satisfied, so:

\frac{\partial h_{i}}{\partial t} + \nabla_{s} \cdot (h_{i} v) = 0, for i = 1, 2, \dots N

The energy equation for a thin film can be written as:

Figure 4. EQUATION_DISPLAY

\sum_{i = 1}^{N} ρ_{i} C_{p_{i}} h_{i} [\frac{\partial T}{\partial t} + (v \cdot \nabla_{s} T)] = \sum_{i = 1}^{N} (k_{i} h_{i} \nabla_{s}^{2} T + h_{i} T_{i} : \nabla_{s} v) - [q_{conv} + q_{rad}]

(748)

where:

$C_{p_{i}}$ is the specific heat capacity of the $i$ th fluid.
$T$ is the temperature.
$k_{i}$ is the thermal conductivity of the $i$ th fluid.
$q_{conv}$ and $q_{rad}$ are the respective convection and radiation heat flux through the top and bottom boundaries of the thin film.
$\begin{matrix} q_{conv} = h_{c} (T - T_{\infty}) \\ q_{rad} = σ ϵ (T^{4} - T_{\infty}^{4}) \end{matrix}$
where:
- $T_{\infty}$ is the ambient temperature.
- $h_{c}$ is the overall convective heat transfer coefficient of the thin film, both top and bottom surfaces.
- $σ$ is the Boltzmann constant.
- $ϵ$ is the emissivity factor.

The material properties of the polymer and solvent are a function of temperature according to an appropriate time-temperature superposition law (for example, Arrhenius, WLF or Nahme's law).