A Body Spinning in an Interfacing Medium

In this case, a solid body spins rapidly in an interfacing fluid medium. Convection, conduction, and radiation operate within in the fluid. Conduction and radiation operate within the solid. The interface is opaque to radiation.

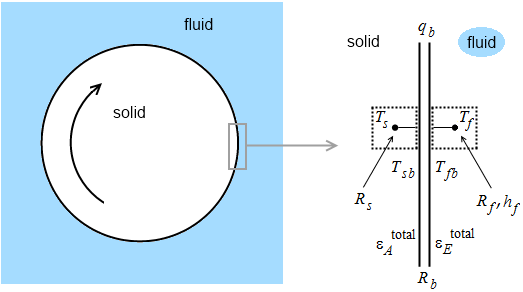
Using averaging, the boundary energy balance for the fluid-side interface is:

Figure 1. EQUATION_DISPLAY

\begin{matrix} (\bar{h_{f} T_{f}} - \bar{h_{f}} T_{f b}) + \bar{(T_{f} / R_{f})} - \bar{(1 / R_{f})} T_{f b} + \bar{q_{af}} - σ {ε_{E}}^{total} {T_{f b}}^{4} \\ = - \frac{q_{b}}{2} + \frac{(T_{f b} - T_{s b})}{R_{b}} \end{matrix}

(1817)

where:

The overline bar indicates averaging. The average value of a variable $x$ is weighted by boundary face area $A$ over a given axial strip $n$ :
$\bar{x} = \frac{\sum_{strip}^{} x_{n} \times A_{n}}{\sum_{strip}^{} A_{n}}$
$h_{f}$ is the convection coefficient of the fluid side.
$T_{f}$ is the cell-center temperature on the fluid side.
$T_{f b}$ is the fluid-boundary temperature.
$T_{s b}$ is the solid-boundary temperature.
$R_{f}$ is the thermal resistance from the fluid cell center to the boundary.
$q_{af}$ is the radiation heat flux in the fluid due to absorption.
$σ$ is the Stefan-Boltzmann constant.
${ε_{E}}^{total}$ is the total boundary emissivity.
$q_{b}$ is the heat flux in the interface.
$R_{b}$ is the thermal resistance of the boundary.

On the left-hand side of Eqn. (1817):

$(\bar{h_{f} T_{f}} - \bar{h_{f}} T_{f b})$ is the convection term.
$\bar{(T_{f} / R_{f})} - \bar{(1 / R_{f})} T_{f b}$ is the conduction term.
$\bar{q_{a f}} - σ {ε_{E}}^{total} {T_{f b}}^{4}$ is the radiation term.

On the right-hand side of Eqn. (1817), the term $\frac{(T_{f b} - T_{s b})}{R_{b}}$ implies conduction through the boundary.

The boundary energy balance for the solid is:

Figure 2. EQUATION_DISPLAY

\frac{1}{R_{s}} (T_{s} - T_{s b}) + q_{a s} - σ {ε_{A}}^{total} {T_{s b}}^{4} = - \frac{q_{b}}{2} + \frac{(T_{f b} - T_{s b})}{R_{b}}

(1818)

where:

$R_{s}$ is the thermal resistance from the solid cell center to the boundary.
$T_{s}$ is the cell-center temperature on the solid side.
$q_{a s}$ is the radiation heat flux in the solid due to absorption.
${ε_{A}}^{total}$ is the total boundary absorbtivity.

On the left-hand side of Eqn. (1818):

$\frac{1}{R_{s}} (T_{s} - T_{s b})$ is the conduction term. 
$q_{a s} - σ {ε_{A}}^{total} {T_{s b}}^{4}$ is the radiation term.

For both equations, assume $T_{f} > T_{f b} > T_{s b} > T_{s}$ .