Solar Radiation

Thermal radiative exchange with the solar environment includes both direct and diffuse components.

The direct solar flux is the irradiation from the sun incident directly on the regions without interference from the atmosphere or other objects. It is modeled as a collimated source as given by $J_{dir, source, λ}$ in Eqn. (1701). Diffuse solar radiation results from the atmospheric scattering, and reflection and transmission from objects such as the ground. It is modeled as a diffuse source $J_{d, source, λ}$ in Eqn. (1701).

The coordinate system for the orientation of the direct solar flux is defined in the following figure:

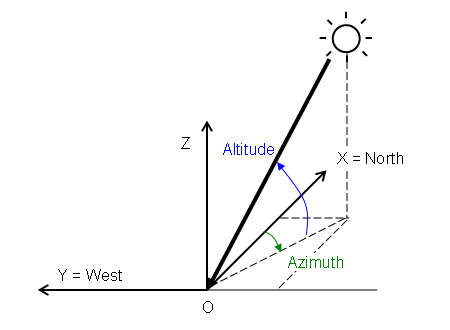
The X-axis is aligned with the local magnetic north direction and the Y-axis is aligned with the local west direction—that is, the XY plane is the local earth-surface plane. The Z-axis then points skyward since Simcenter STAR-CCM+ employs right-handed coordinate systems.

User Input Range for the Solar Calculator

The solar calculator is a set of equations that calculate the astronomical relationship between sun, earth, and the atmosphere. It is developed by the National Renewable Energy Laboratory (NREL) [420]. This formulation presents the equations for solar position and flux calculations in the solar calculator. The user inputs for various parameters must lie within the ranges that are shown in the following table .

All angles that are shown in this formulation are in degrees.


Variable		Range
Year		1950-2050
Month		1-12
Day		1-31 (depending on the month)
Hour		0 – 23
Minute		0-59
Time zone		-12.0 -+12.0 (in hours)
Latitude		- 90.0-+90.0 (in degrees)
Longitude		-180.0-+180.0 (in degrees)
Fraction for diffuse flux		0.0-1.0
Sunshine factor		0.0-1.0

Calculation of Sun Direction

Solar altitude, azimuthal angles, and related geometric parameters can be calculated as:

Day angle [421]:
Figure 1. EQUATION_DISPLAY

$α_{d} = \frac{360 °}{365} (d_{y e a r} - 1)$

(1773)

where $d_{y e a r}$ is the day of the year.
Earth radius vector [422]:
Figure 2. EQUATION_DISPLAY

$r_{E} = 1.000110 + 0.034221 \cos (α_{d}) + 0.001280 \sin (α_{d}) + 0.000719 \cos (2 α_{d}) + 0.000077 \sin (2 α_{d})$

(1774)

Coordinated Universal Time (UTC) in hours:

Figure 3. EQUATION_DISPLAY

U T C = h o u r + \frac{m i n u t e}{60} - t i m e Z o n e

(1775)

Julian day [423]:

Figure 4. EQUATION_DISPLAY

d_{j u l} = 32916.5 + 365 (y e a r - 1949) + \frac{y e a r - 1949}{4} + d_{y e a r} + \frac{U T C}{24}

(1776)

Time that is used in calculation of elliptical coordinate [423]:

Figure 5. EQUATION_DISPLAY

t_{e c} = d_{j u l} - 51545.0

(1777)

Mean longitude [423]:

Figure 6. EQUATION_DISPLAY

L_{m} = 280.460 + 0.9856474 t_{e c} (0 ° \leq L_{m} \leq 360 °)

(1778)

Mean anomaly [423]:

Figure 7. EQUATION_DISPLAY

A_{m} = 357.528 + 0.9856003 t_{e c} (0 ° \leq A_{m} \leq 360 °)

(1779)

Elliptic longitude [423]:

Figure 8. EQUATION_DISPLAY

L_{e} = L_{m} + 1.915 \sin (A_{m}) + 0.020 \sin (2 A_{m}) (0 ° \leq L_{e} \leq 360 °)

(1780)

Obliquity of the elliptic [423]:

Figure 9. EQUATION_DISPLAY

O_{e} = 23.439 - (4 \times 10^{7}) t_{e c}

(1781)

Declination [423]:

Figure 10. EQUATION_DISPLAY

D_{c} = {sin}^{-1} {\sin (O_{e}) \sin (L_{e})}

(1782)

Right ascension [423]:

Figure 11. EQUATION_DISPLAY

R_{a} = {tan}^{- 1} {\frac{\cos (O_{e}) \sin (L_{e})}{\cos (L_{e})}} (0 ° \leq R_{a} \leq 360 °)

(1783)

Greenwich mean sidereal time [423]:

Figure 12. EQUATION_DISPLAY

t_{g m t} = 6.697375 + 0.0657098242 t_{e c} + U T C (0 \leq t_{g m t} \leq 24)

(1784)

Local mean sidereal time [423]:

Figure 13. EQUATION_DISPLAY

L_{m s t} = {15 t}_{g m t} + L_{o} (0 ° \leq L_{m s t} \leq 360 °)

(1785)

where $L_{o}$ is the user-defined longitude of the geographical location.

Hour angle [423]:

Figure 14. EQUATION_DISPLAY

β_{h} = L_{m s t} - R_{a} (- 18 0 ° \leq β_{h} \leq 180 °)

(1786)

Solar zenith $Z$ and altitude angles without refraction [423]:

Figure 15. EQUATION_DISPLAY

Z = {cos}^{-1} {\sin (D_{c}) \sin (L_{a}) + \cos (D_{c}) \cos (L_{a}) \cos (β_{h})} (0 ° \leq Z \leq 99 °)

(1787)

where $L_{a}$ is the user-defined latitude of the geographical location. $Z$ is limited to 9 degrees below the horizon to compensate for refraction.

Altitude:

Figure 16. EQUATION_DISPLAY

θ = 90 ° - Z

(1788)

Solar azimuthal angle [423]:

Figure 17. EQUATION_DISPLAY

ϕ = 180 ° - {cos}^{-1} {\frac{\sin (θ) \sin (L_{a}) - \sin (D_{c})}{\cos (θ) \cos (L_{a})}} i f β_{h} > 0 °, ϕ = 360 ° - ϕ

(1789)

Application of Refraction Correction

The refraction correction [424] is applied as follows:

$c f$ is the correction factor due to atmospheric refraction.

Figure 18. EQUATION_DISPLAY

c f = 0 if θ > 85 °

(1790)

Figure 19. EQUATION_DISPLAY

c f = \frac{58.1}{\tan (θ)} - \frac{0.07}{\tan^{3} (θ)} + \frac{0.000086}{\tan^{5} (θ)} if 5 ° \leq θ \leq 85 °

(1791)

Figure 20. EQUATION_DISPLAY

\begin{matrix} c f = 1735 + θ [- 518.2 + θ {103.4 + θ (- 12.79 + 0.711)}] \\ if - 0.575 ° \leq θ < 5 ° \end{matrix}

(1792)

Figure 21. EQUATION_DISPLAY

c f = \frac{20.774}{\tan (θ)} if θ < - 0.575 °

(1793)

Figure 22. EQUATION_DISPLAY

c f = (\frac{c f}{3600}) (\frac{283 P}{1013 (273 + T)})

(1794)

where $P$ equals 1013 millibars atmospheric pressure and $T$ equals $15 ° C$ mean atmospheric temperature.

Refraction corrected altitude:

Figure 23. EQUATION_DISPLAY

θ_{r} = θ + c f (- 9 ° \leq θ_{r} \leq 90 °)

(1795)

Refraction corrected zenith:

Figure 24. EQUATION_DISPLAY

Z_{r} = 90 - θ_{r}

(1796)

Calculation of Solar Fluxes

Total solar flux:

Figure 25. EQUATION_DISPLAY

q = C_{s} r_{E} (\cos (Z_{r})) f_{s} if \cos (Z_{r}) > 0

(1797)

Figure 26. EQUATION_DISPLAY

q = 0 if \cos (Z_{r}) \leq 0

(1798)

where $C_{s}$ is the solar constant, equal to 1376.0 $W / m^{2}$ , and $f_{s}$ is the sunshine factor.

Diffuse flux:

Figure 27. EQUATION_DISPLAY

q_{d i f f} = {q f}_{d i f f}

(1799)

where $f_{d i f f}$ is the diffuse factor.

Direct flux:

Figure 28. EQUATION_DISPLAY

q_{d i r} = q (1.0 - f_{d i f f})

(1800)