Radiative Properties

Spectral Modeling of Thermal Radiation

Simcenter STAR-CCM+ uses the thermal radiation model to define how thermal radiation properties are modeled—either as wavelength independent (gray) or as wavelength dependent (spectral). The choice pertains uniformly to all radiation within the regions of the simulation and in the surrounding environment. The thermal radiation model is responsible for managing the radiative properties and the spectrum-dependent solution variables in the continuum.

The gray thermal radiation model accounts for diffuse and specular radiation independent of wavelength. The radiation properties of the media and the surrounding surfaces are considered the same for all wavelengths.

The multiband thermal radiation model lets you simulate diffuse and specular radiation that is dependent on wavelength or frequency. With this model, wavelength bands specify radiation properties of the media and surrounding surfaces. The number and extents of bands are chosen to describe property variations with respect to wavelength. During the solution process, the governing radiation equations are solved for each defined band using the specified properties. The total radiation solution is then obtained by integrating (summing) the solutions from each of the individual bands. Since the governing equations are solved for each band, the radiation solution time generally increases linearly with the number of bands. As a consequence, a trade-off often exists between accuracy and computational time.

Radiative Properties of Surfaces

Surface properties are defined at the boundary level within Simcenter STAR-CCM+.

Absorptivity

Absorption is a phenomenon that describes energy being removed from the incident radiative energy by the material or the boundary. Absorptivity is dimensionless and is defined as:

$${\alpha }_{\lambda }=\frac{q_r^{abs}}{I_{f,\lambda }}$$

(1762)

where $q_r^{abs}$ is the radiative energy that is absorbed and $I_{f,\lambda }$ is the total radiative energy incident on a boundary. From Kirchhoff's law, the spectral directional emissivity is equal to the spectral directional absorptivity. In Simcenter STAR-CCM+, directional properties are not used. Therefore, Kirchhoff's law is implemented as:

$${ϵ}_{\lambda }={\alpha }_{\lambda }$$

(1763)

where ${ϵ}_{\lambda }$ is the spectral emissivity and ${\alpha }_{\lambda }$ is the spectral absorptivity. For a gray model, the properties are independent of both direction and wavelength, and emissivity equals absorptivity for the entire spectrum.

Transmissivity

Transmissivity ${\tau }_{\lambda }$ is dimensionless and is defined as:

$${\tau }_{\lambda }=\frac{{\dot{q}}_r^{trans}}{I_{f,\lambda }}$$

(1764)

where ${\dot{q}}_r^{trans}$ is the transmitted radiant energy and $I_{f,\lambda }$ is the incident radiant energy at a given surface.

Reflectivity

Reflectivity ${\rho }_{\lambda }$ is defined as:

$${\rho }_{\lambda }=\frac{{\dot{q}}_r^{refl}}{I_{f,\lambda }}$$

(1765)

where ${\dot{q}}_r^{refl}$ is the reflected radiant energy.

Surface reflectivity can be partially or fully specular (as opposed to diffuse). A perfectly specular surface is one where the direction of incoming light is perfectly reflected across the surface normal. The angle of incidence ${\theta }_i$ is equal to the angle of reflection ${\theta }_r$as is shown in the following diagram: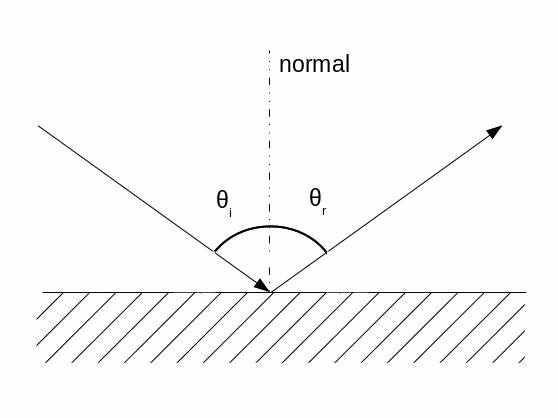

Reflection specularity is the specular fraction of the surface reflectivity. A value of 0 denotes that all of the reflection is diffuse, whereas a value of 1 denotes that all of the reflection is specular. Values between 0 and 1 indicate partial specularity. Specular reflectivity is then determined from the product of reflection specularity and surface reflectivity. A special case is that of a mirrored surface that is represented by setting the surface reflectivity and the reflection specularity to 1. This setting means that the surface is completely reflective and that all of the reflection is specular. In this case, the specular reflectivity is also equal to 1. Alternatively, specular reflective surfaces an also be partially transmissive, for example, plate glass or particularly low-emissivity glas and/or they can be absorptive such as high-gloss-painted surface. In such cases, the surface reflectivity is less than 1 with surface transmissivity and/or surface emissivity making up the difference to satisfy Kirchhoff's law.

Radiative Properties of Participating Media

As radiation travels through a medium, the intervening material absorbs and increments its radiant intensity $I$ in the $\mathrm{\Omega }$ direction. The radiative transfer equation (RTE) Eqn. (1721) governs this process.

Absorption Coefficient

Absorption is a phenomenon that describes energy being removed from the incident radiative energy by the material. This phenomenon is described using the absorption coefficient $k$. Incoming intensity is linearly decremented by $k$ along a line of sight according to:

$$\frac{d{I}_{\lambda ,abs}}{ds}=-k{I}_{\lambda }$$

(1766)

In local thermodynamic equilibrium conditions, Kirchhoff's law applies. The volumetric emission is proportional to the absorption coefficient and the blackbody function. The local intensity along a line of sight is augmented following:

$$\frac{d{I}_{\lambda ,em}}{ds}=k{I}_{b,\lambda }$$

(1767)

where $I_{\lambda ,em}$ is blackbody emission intensity along the line of sight at wavelength $\lambda$.

Scattering Coefficient

The scattering coefficient is the property of a medium that describes the amount of scattering of thermal radiation per unit path length within the medium. Scattering in Simcenter STAR-CCM+ is isotropic for both continuum and particle radiation.

Refractive Index

The refractive index governs local emission and the direction as is described in Refractive Index and Blackbody Intensity and Refraction, Reflection, and Critical Angle.

In Simcenter STAR-CCM+, refraction is only considered at the interface between two media. Therefore, refraction is specified for each medium.

When the absorption and the scattering coefficients as well as the refractive index of the medium are independent of wavelength, the medium is called gray. In that case, the RTE can be integrated over wavelength (or, equivalently, wavenumber) to produce a wavelength-independent equation. If the properties vary across the spectrum, a multiband thermal model can be used to model the spectral variability.

Weighted Sum of Gray Gases Method (WSGGM)

Simcenter STAR-CCM+ employs the weighted sum of gray gases method (WSGGM) to model radiative heat transfer properties in participating media that are gas mixtures consisting of ${\text{CO}}_2$ and ${\text{H}}_2\text{O}$. WSGGM is widely used in the simulation of air-fuel combustion processes.

Combustion product gases do not scatter radiation significantly, but are strong selective emitters and absorbers of radiation. ${\text{CO}}_2$ and ${\text{H}}_2\text{O}$ gases dominate cloud emission and absorption among the combustion gas products. These species require that the spectral variation of radiative properties is accounted for.

The weighted sum of gray gases (WSGG) method for calculating the absorption coefficient is a reasonable compromise between the oversimplified user-provided gray gas model and a complete spectral property model which takes into account detailed absorption bands. This method uses the Hottel charts [406] and sum-of-gray-gases models [407] for a mixture containing ${\text{CO}}_2$ and/or ${\text{H}}_2\text{O}$ gases only. Several curve-fitted sum-of-gray-gases expressions are available [402]. In the WSGG method, the medium is assumed to consist of different fractions of gray gases with different absorption coefficients.

The relationship between the total gray gas absorption coefficient $\kappa$ and the total absorptivity $\alpha$ for a gray medium is the Bouguer-Lambert law:

$$\alpha =1-e^{-\kappa s}$$

(1768)

where $s$ is the optical path length (OPL).

The total absorptivity is approximated with a weighted-sum of several gray gases as:

$$\alpha \approx {\displaystyle \sum _{k=0}^K}{a}_k\left(1-e^{-{\kappa }_{k}s}\right)$$

(1769)

where $K$ is the total number of gray gases, $a_k$ is the weight factor and ${\kappa }_k$ is the absorption coefficient of each gray gas. Based on the quality of the curve-fit of Hottel charts [406] and sum-of-gray-gases models [407], typically $K=3$ gives satisfactory accuracy. Simcenter STAR-CCM+ always uses this value of $K$.

After computing $\alpha$ from Eqn. (1769), the total gray gas absorption coefficient $\kappa$ is obtained using the Bouger-Lambert Law (Eqn. (1768)). $\kappa$ is then used to solve the RTE as $k_a$.

The OPL is a user-provided quantity. The OPL can be used as a tuning parameter to get the expected and reasonable distribution for the absorption coefficient of the gas medium. The OPL value can range from the cell dimensions to the dimension of the entire computational domain, depending on the optical thickness of the combustion region. For instance, if the optical thickness of the combustion medium is high then the cell thickness can be used to define the OPL. However, for an optically thin medium, use a value that corresponds to the reactor dimension.

The OPL is related to optical thickness by:

$$\theta =s\kappa$$

(1770)

where $\theta$ is the optical thickness, $s$ is the OPL, and $\kappa$ is the absorption coefficient.

Once a value of the OPL is prescribed, the WSGG method captures local variation of the absorption coefficient (which is due to variation in the gas temperature and partial pressures of combustion gases).

For arbitrary geometries, the OPL can be approximated as [408]:

$$s=3.6\text{ (volume/surface area)}$$

(1771)

where the volume is the total volume of the gas and the surface area is its total surface area.

Correlated k-Distribution Method

The correlated k-distribution gray gases method is a refinement of the WSGGM. It provides a smoother set of weight functions and so is more easily integrated, though at a higher computational cost. The method uses a spectral reordering method for specifying the absorption coefficients of gaseous H₂O and CO₂. The method was originally developed to model line emission and absorption of vibration-rotation bands; these are of principal importance in combustion applications. CO₂ and H₂O have thousands of bound-bound line transitions which are broadened due to pressure broadening and Doppler effects. The following figure (from [411]) shows the absorption coefficient of CO₂ over a narrow spectral band for two representative states.

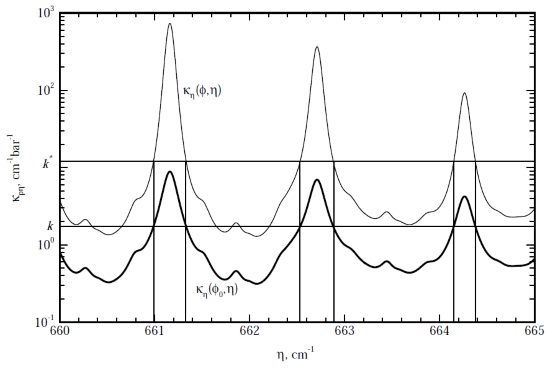
Resolving the spectral variation for the many lines of the combustion gases requires many spectral points for accuracy, in the Line-by-Line method. If the spectral variation of the absorption coefficient is the same throughout the medium (i.e. it is a homogeneous medium), then the same radiative transfer (RTE) equations are solved for many times. The k-distribution method reorders the spectrum into a monotonically increasing function, greatly reducing the number of RTE solutions required, and for a homogeneous mixture provides Line-by-Line accurate results. Modest [411] defines a k-distribution (for a narrow band) as:

$$f(\mathbf{\varphi },k)=\frac{1}{\mathrm{\Delta }\lambda }{\int }_{\mathrm{\Delta }\lambda }^{}\delta (k-k_a(\mathbf{\varphi },\lambda ))d\lambda$$

(1772)

where:

• $\mathbf{\varphi }$ is a vector representing the properties of the gas (temperature, pressure, mole fraction).
• $k_a(\mathbf{\varphi },\lambda )$ is the spectral absorption coefficient of the gas.
• $\delta (k-k_a(\mathbf{\varphi },\lambda ))$ is the Dirac delta function.

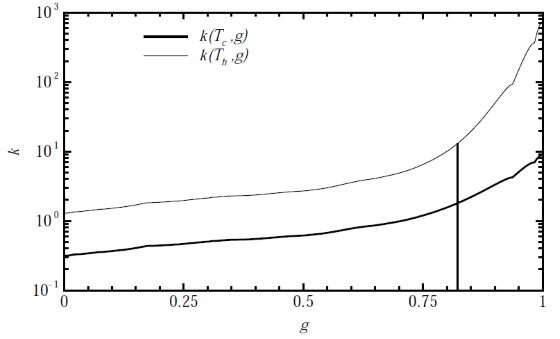
The k-distribution is a probability density function, giving the probability that the absorption coefficient will attain a value of k. The cumulative distribution is given by:

where $g$ represents a fraction of the spectrum with absorption coefficient $k_{a\lambda }<k$, as shown in following figure (from [411]) for the narrow band depicted in the previous figure:

When considering a broader spectral region (full spectrum), the variation of the Planck function at different temperatures must be taken into account. The function $f$ becomes:

where $I_b$ is total, spectrally integrated blackbody intensity and $I_{b\lambda }$ is blackbody intensity at wavelength $\lambda$ .

The function $g$ then becomes:

where $g$ represents the Planck-function-weighted fraction of the spectrum. The correlations of Modest and Mehta [413] and Modest and Singh [415] are used to calculate the full spectrum $k-g$ distributions for CO₂ and H₂O respectively. The mixing rules of Modest and Riazzi [414] are used to combine the $k-g$ distributions if both species are present.