Sampling Methods for DOE Studies

Design of Experiment (DOE) studies require a population of input parameters within a certain range without any extra parameter distribution.

For a DOE study, the following sampling methods are available:


Sampling Method	Designs to Run	Suitability	Design Point Distribution
2-Level Full Factorial	$2^{n}$ $n$ is the number of input parameters	Computing the main and interaction effects	Mainly on edges or corners of the design space
3-Level Full Factorial	$3^{n}$ $n$ is the number of input parameters	Computing the main and interaction effects	Mainly on edges or corners of the design space
Latin Hypercube Sampling (Optimal)	Chosen by user	Building response surface	Uniformly distributed in the design space

2-Level Full Factorial

A 2-level full factorial design specifies the range of each input parameter with two values (levels)— Low and High. For $n$ input parameters, the total number of design runs is $2^{n}$ , in which all value combinations are investigated.

3-Level Full Factorial

A 3-level full factorial design specifies the range of each input parameter with three values (levels)— Low, Mid, and High. For $n$ input parameters, the total number of design runs is $3^{n}$ , in which all value combinations are investigated.

Latin Hypercube Sampling (Optimal)

This type of DOE study requires you to choose the Parameter Type:

Constant—You specify a constant value for this input parameter without exploring other values.
Discrete—You can specify several values for this input parameter separated with commas or spaces. Those values are used, when possible, equally in the design runs.
Continuous—You specify a value range for this input parameter.

If the Parameter Type is set to Continuous, the Latin Hypercube Sampling method selects the values within the continuous range of this input parameter.

Within DOE settings, you specify the number of Designs to Run. If there are $m$ Designs to Run (sample size), the range of each continuous input parameter is divided equally into $m$ intervals. Design Manager selects one value from each interval.

When there are multiple input parameters the number of designs increases. In order to maintain efficiency, from the randomly generated samples, the Latin Hypercube sampling algorithm chooses value combinations that provide a uniform distribution in the design space.

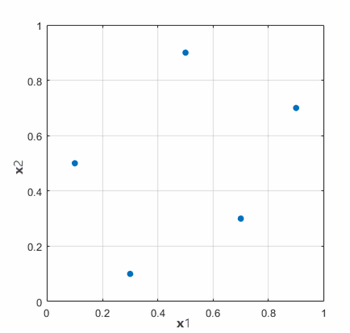
For example, if you have two input parameters $x_{1} \in [0, 1]$ and $x_{2} \in [0, 1]$ and 5 designs to run, an initial random sampling might result in the set of design studies shown in the following plot:

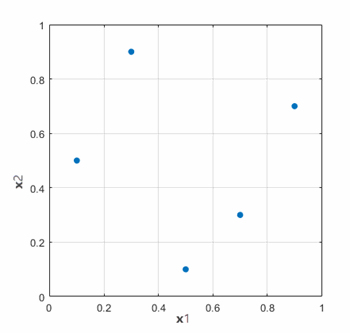
In the initial distribution, sample points 3 and 4 are relatively close to each other. The Latin Hypercube algorithm checks the uniformity of the design points distribution and improves the choice of samples. For this example, the Latin Hypercube method adjusts the sample points as follows: