Crystallization

A Solute Crystallization model and a Melt Crystallization model are implemented in Simcenter STAR-CCM+.

Nucleation

The simplest form of spatially homogeneous population balance equation (PBE) reads:

Figure 1. EQUATION_DISPLAY

\partial_{t} n = - \partial_{L} (2 G n) + {\dot{N}}_{0} δ (L - L_{0})

(2406)

where:

$n (L)$ is the particle size distribution (PSD), the number density of particles of diameter $L$ .
$G = \frac{1}{2} \partial_{t} L$ is the growth rate accounting for the phase change at the surface of a particle.
${\dot{N}}_{0}$ is the nucleation rate.
$L_{0}$ is the nucleus diameter.

Concentration of the solute in the solution, $C_{l}$ , is governed by the advection-diffusion-reaction equation:

Figure 2. EQUATION_DISPLAY

\partial_{t} ρ_{l} α_{l} C_{l} + \nabla\cdot ρ_{l} α_{l} (C_{l} u_{l} - D_{T} \nabla C_{l}) = - S_{c}

(2407)

where the sink term, $S_{c}$ , is given by integration of the surface growth rate over entire particle-liquid interface and creation of new particles:

Figure 3. EQUATION_DISPLAY

S_{c} = π \int ρ_{s} n (L) L^{2} G d (L) + ρ_{s} {\dot{N}}_{0} \frac{π}{6} L_{0}^{3}

(2408)

The schematic diagram below shows the mass and energy balance for a particle:

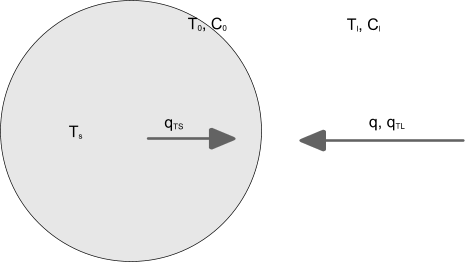
The interior of the particle has a temperature $T_{s}$ . At the interface, the concentration of the solute is $C_{0}$ and its corresponding temperature is $T_{0}$ . In the liquid, the temperature is $T_{l}$ and the concentration of the solute is $C_{l}$ . The mass flux of the solute to the surface, $q$ , is balanced by the crystal growth rate, $ρ_{s} G$ . Heat is transported to the surface from the liquid and from the interior of the particle: the corresponding fluxes are $q_{T L}$ and $q_{T S}$ .

The mass and energy balance read:

Figure 4. EQUATION_DISPLAY

q = ρ_{s} G

(2409)

Figure 5. EQUATION_DISPLAY

q_{T L} + q_{T S} = - q H_{c}

(2410)

where $H_{c}$ is the enthalpy of crystallization.

Generally speaking, Eqn. (2409) and Eqn. (2410) are appropriate to almost every mass transfer process (for example, boiling, heterogeneous combustion). However, numerical considerations and user convenience require further differentiation of the models.

A distinction can be made between concentration-driven (solute) crystallization and temperature-driven (melt) crystallization (Mullin, [522]).

Solute Crystallization

In a solute crystallization process, a compound (the solute) is dissolved in another liquid (the solvent). When the temperature drops, or an anti-solvent is added, the concentration of the solute becomes higher than the saturation concentration and crystallization starts.

The surface growth rate $G$ is a function of the supersaturation (Mullin, [522]; Borissova, [434]):

Figure 6. EQUATION_DISPLAY

G = k_{g} {(Δ C)}^{m_{g}}

(2411)

where $k_{g}$ (the prefactor) and $m_{g}$ (the exponent) are empirical parameters.

The saturation concentration $C_{s a t} (T)$ is a function of the temperature. The supersaturation delta $Δ C = C_{0} - C_{s a t}$ is the difference between the solute concentration in the liquid film around the particle and the saturation concentration.

Usually, dissolution is a faster process than crystallization (Mullin, [522]), so the parameters of Eqn. (2411) are demarcated:

Figure 7. EQUATION_DISPLAY

k_{g} = {\begin{matrix} k_{g}^{+}, & C_{s a t} \geq 0 \\ k_{g}^{-}, & C_{s a t} < 0 \end{matrix}

(2412)

Figure 8. EQUATION_DISPLAY

m_{g} = {\begin{matrix} m_{g}^{+}, & C_{s a t} \geq 0 \\ m_{g}^{-}, & C_{s a t} < 0 \end{matrix}

(2413)

The phase change is balanced by corresponding mass transfer to the film; the mass balance is:

Figure 9. EQUATION_DISPLAY

q = ρ_{s} G = ρ_{l} S h \frac{D}{L} (C_{l} - C_{0})

(2414)

where:

$q$ is the mass flux
$S h$ is the Sherwood number
$D$ is the coefficient of molecular diffusion
$ρ_{s}$ and $ρ_{l}$ are densities of the solid and liquid phases, respectively.

The energy balance for the film includes both internal and external heat transfer, as follows:

Figure 10. EQUATION_DISPLAY

N u \frac{λ_{l}}{L} (T_{l} - T_{0}) = F o \frac{λ_{s}}{L} (T_{0} - T_{s}) - q H_{c}

(2415)

where:

$N u$ is the Nusselt number
$F o$ is the Fourier number
$λ_{l}$ and $T_{l}$ are the heat conductivity and temperature of the liquid phase
$λ_{s}$ and $T_{s}$ are the heat conductivity and temperature of the solid phase.

The Simcenter STAR-CCM+ implementation follows that of other models (for example, evaporation) and assumes that $F o = \infty$ , that is $T_{0} = T_{s}$ .

Melt Crystallization

Unlike its solute counterpart, melt crystallization can occur in a single-component liquid (for example, ice formation in water). Admixtures that are dissolved in the liquid are also important. Firstly, admixtures lower the saturation temperature. For example, the freezing temperature of sea water is lower than the freezing temperature of fresh water. Secondly, the composition of the crystals is different from the composition of the melt. For example, melt crystallization processes are important in the food industry and in water desalination (Rahman, [530], Casenave, [438]).

The growth rate is given by the following formula (Mullin, [522]):

Figure 11. EQUATION_DISPLAY

G = {\begin{matrix} k_{g}^{+} {(Δ T)}^{m_{g}^{+}} C_{0}, & Δ T \geq 0 \\ k_{g}^{-} {(Δ T)}^{m_{g}^{-}}, & Δ T < 0 \end{matrix}

(2416)

where $Δ T = T_{0} - T_{s a t}$ is temperature supersaturation. As for solute crystallization, the melting (dissolution) is usually faster than the crystal growth, so the parameters of Eqn. (2416) are split into two sets.

The growth depends on the concentration of the freezing component on the surface of the crystal, the melting is concentration-independent because the crystal is assumed to be single-component. An additional simplification is made in the current implementation of the melt crystallization model: it is assumed that $C_{0} = C_{l}$ . This assumption (Casenave, [438]) is justified for high mass transfer rates and (or) slow growth rates.

The mass and energy balances for melt crystallization are:

Figure 12. EQUATION_DISPLAY

q = ρ_{s} G

(2417)

Figure 13. EQUATION_DISPLAY

q_{T S} = N u \frac{λ_{l}}{L} (T_{s} - T_{l}) - q H_{c}

(2418)

Armenante-Kirwan Correlations

The standard Ranz-Marshall correlations for the Nusselt number and the Sherwood number assume that the heat and mass transfer are amplified by mean interphase slip velocity. For small particles, the mean slip is small, but experiments suggest that the transfer is enhanced by turbulence. A model for mass transfer to micro-particles has been proposed by Armenante and Kirwan ([428]).

A number of similar models have been reported in the literature (Pangarkar, [527]). However, given the uncertainty in the experimental data, Simcenter STAR-CCM+ implements a new model with user-controlled parameters:

Figure 14. EQUATION_DISPLAY

N u = 2.0 + α {Re}_{T}^{β} \Pr^{γ} {(\frac{Δ ρ}{ρ_{l}})}^{δ}

(2419)

Figure 15. EQUATION_DISPLAY

S h = 2.0 + α {Re}_{T}^{β} {S c}^{γ} {(\frac{Δ ρ}{ρ_{l}})}^{δ}

(2420)

where the turbulent Reynolds number, ${Re}_{T}$ , is:

Figure 16. EQUATION_DISPLAY

{Re}_{T} = \frac{ϵ^{1 / 3} L^{4 / 3}}{ν}

(2421)

where $ϵ$ is the power input per unit mass of fluid.

The default values of the coefficients are $α = 0.52$ , $β = 0.52$ , $γ = 0.333$ , $δ = 0.0$ .

These values can be user-specified. See Sherwood Number Properties and Nusselt Number Properties.