Working with Secondary Breakup
Liquid droplets sometimes break up under the action of non-uniform surface forces, a phenomenon that is known as secondary breakup.
The response of droplets to non-uniform surface forces is invariably to deform, with the deformation resisted by surface tension and viscous forces inside the droplet. Characteristic measures of this behavior are the Weber and Ohnesorge numbers
Depending on the magnitude of these forces, various breakup regimes have been identified, each characterized by the shape of the deforming droplets. An example categorization (after Stiesch [708]) for low Oh is given below.
| Category | Weber Number | |
|---|---|---|
| Vibrational breakup |
 |
~ 12 |
| Bag breakup |
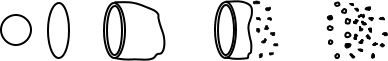 |
< 20 |
| Bag/ streamer breakup |
 |
< 50 |
| Stripping breakup |
 |
< 100 |
| Catastrophic breakup |
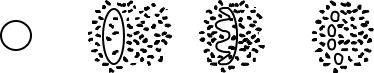 |
> 100 |
Other categorizations identify more or fewer regimes; the above is representative.
Detailed modeling of even one breakup regime is difficult. At most, the goal of secondary breakup models is to predict when breakup occurs and what diameters result from it. A selection of models is provided in Simcenter STAR-CCM+:
- KHRT (stripping, catastrophic)
- Reitz-Diwakar (bag, stripping)
- TAB (vibrational)
- SSD (catastrophic)
The most appropriate regime for each model is noted in parentheses. However it is not unusual to find models that are applied outside these regimes. Where possible, results from more than one breakup model can be compared to add confidence.
These models become available when the Gas, Liquid, Multiphase, Multi-Component Gas, or Multi-Component Liquid model is selected.