Laminated Steel Model Reference

Laminated steel is a common material for the constituent parts in electric motors and transformers. It consists of thin layers of steel coated in a insulating layer, which prevents eddy currents from passing between the layers.

As the primary purpose of laminating steel is to disrupt the eddy currents, the laminations are stacked so the component of the magnetic field normal to the lamination plane is as small as possible.

Eddy currents within laminated steel are a superposition of two modes based on the loop orientation:

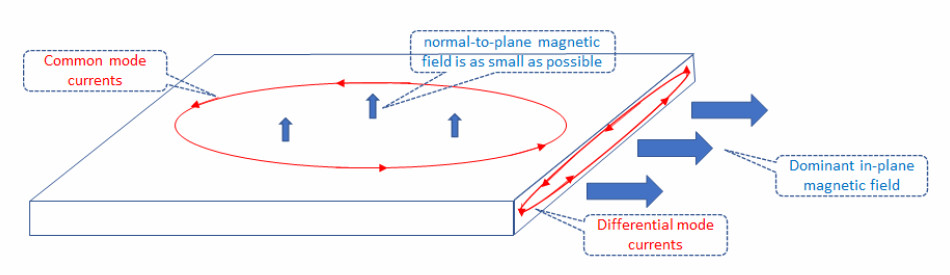
Common Mode—electric current loops in planes parallel to the lamination plane. They are generated by alternating normal-to-plane magnetic fields that are usually small in well designed machines.
Differential Mode—electric current loops in planes perpendicular to the lamination plane. They are generated by alternating in-plane magnetic fields which are dominant in well designed machines.

In general, dominant differential mode currents require a finer mesh, which is often impractical. The Laminated Steel model captures the dominant differential mode currents without the need for a fine mesh resolution.


Model Name	Laminated Steel
Theory	See Laminated Steel.
Provided By	[physics continuum] > Models > Optional Models
Example Node Path	Continua > Physics 1 > Models > Laminated Steel
Requires	Physics Models: Space: Three Dimensional Time: Implicit Unsteady Material: Solid Optional Models: Electromagnetism and Finite Element Magnetic Vector Potential
Activates	Material Properties	Electrical Conductivity, Lamination Stack, and Magnetic Permeability. See Material Properties.

Material Properties

Electrical Conductivity

Allows you to define the electrical conductivity

σ

using a diagonal tensor (see Eqn. (4324)).

Method	Associated Value Nodes
Transverse Isotropic Lamination	Normal The only available option is Null, which sets $σ_{m z}$ in Eqn. (4324) to zero, providing that the lamination stacking orientation is along the z axis. Transverse Defines $σ_{m y}$ in Eqn. (4324)
Orthotropic Lamination	Normal The only available option is Null, which sets $σ_{m z}$ in Eqn. (4324) to zero, providing that the lamination stacking orientation is along the z axis. Rolling Defines $σ_{m x}$ in Eqn. (4324) Transverse Defines $σ_{m y}$ in Eqn. (4324)

Lamination Stack

Allows you to define the Metal Layer Thickness,

h_{m}

, and the Stacking Factor,

s

, for the laminated steel material (see Eqn. (4328)). The Stacking Factor is the ratio between the total steel metal thickness and the laminated steel thickness. For most laminated steel sheets this value is around 0.95. If the insulation thickness of the laminated sheet is negligible, set this value to 1.0.

Magnetic Permeability

Specifies the magnetic permeability

μ

of the material (see Eqn. (4220)). Typically, for laminated steel materials, you define

μ

using a B-H table. For more information, see Finite Element Magnetic Vector Potential Model Reference.