Fiala Thermoregulation Model

The Fiala Thermoregulation model is a multi-segment, multi-node model that simulates the human body, including predictions of overall and local physiological responses.

The model is based on the average person, with a detailed multi-layered structure of the human body. The environmental heat exchange models local heat losses and gains from the body by free and forced convection, solar irradiation, long-wave radiation, evaporation of moisture from the skin, and the insulation effect of the clothing.

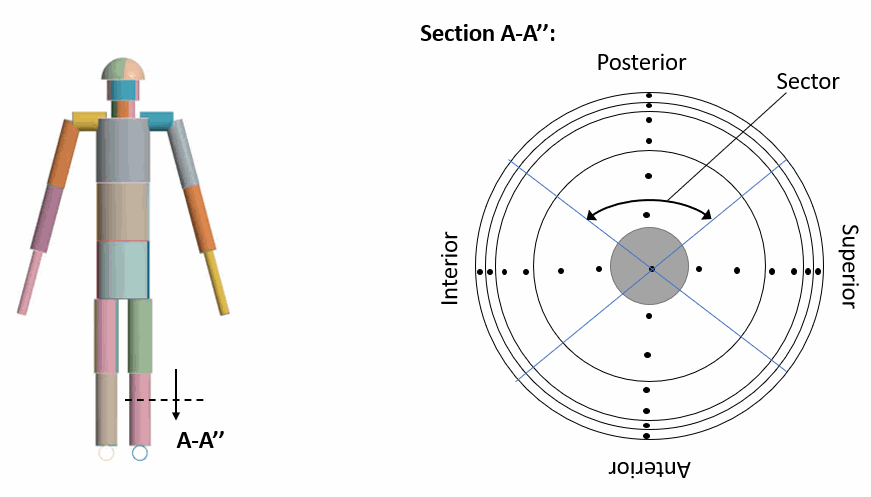
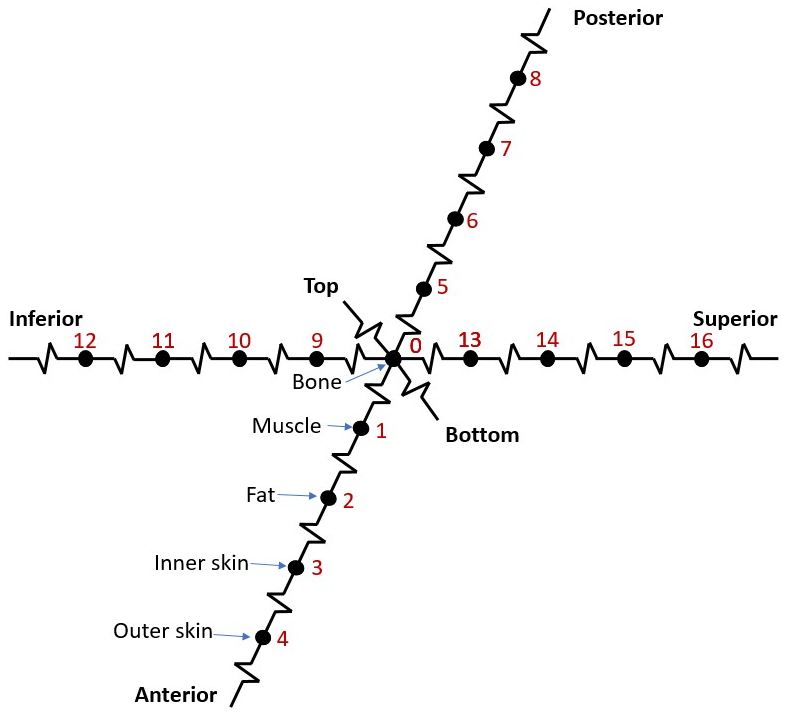
The human body is modeled as cylindrical and spherical (head) body segments built of concentric tissue layers with distinct thermal and physiological properties. Each body segment is also subdivided into tangential sectors to consider asymmetric boundary conditions (for example frontal or lateral directional radiation). The following image shows the segmented body on the left hand side and the radially and tangentially subdivided cross-section A-A'':

The innermost concentric tissue layer is bone (grey circle), followed by muscle, fat, inner skin, and outer skin.

This segment-sector-layer model of body is then modeled as a thermal network with the network nodes on a segment as shown by dots in the cross-section image A-A". The thermal resistances are computed based on the thermal conductivities of each layer material (skin, fat, muscle, bone, and so on) and the geometric dimensions of each tissue lump represented by the network node. The following image shows a representative thermal network for a segment:

Bioheat Equation with Passive and Dynamic Thermoregulation

The Fiala Thermoregulation model solves the bioheat transfer equation to predict the dynamic heat and mass transport in the body [405], considering the effects of the active and passive systems. The largest portion of heat from the human body that is released to the environment is through the skin, although some of the heat is lost through respiration.

The bioheat equation is given by:

Figure 1. EQUATION_DISPLAY

\underset{Unsteady term}{\underset{⏟}{ρ C_{p} \frac{\partial T}{\partial t}}} = \underset{Radial heat conduction}{\underset{⏟}{k (\frac{\partial^{2}}{\partial r^{2}} + \frac{ω}{r} \frac{\partial T}{\partial r})}} + \underset{Blood perfusion heat convection}{\underset{⏟}{ρ_{b l} w_{b l} C_{p, b l} (T_{b l a} - T)}} + \underset{Metabolic heat generation}{\underset{⏟}{q_{m}}}

(1801)

where:

$ρ$ is the tissue density.
$C_{p}$ is the thermal heat capacity of tissue.
$T$ is the tissue temperature.
$k$ is the tissue conductivity.
$t$ is the time.
$ω$ is a geometry factor (1 for polar coordinates, 2 for spheres)
$T_{b l a}$ is the arterial blood temperature.
$ρ_{b l}$ is the density of blood.
$w_{b l}$ is the blood perfusion rate.
$C_{p, b l}$ is the thermal heat capacity of blood.
$q_{m}$ is the metabolic heat generation.

The heat loss due to respiration (negative value) is added to the metabolic heat source term. The heat loss due to evaporation is considered on the skin boundary. Conduction, blood perfusion, respiration, and evaporation are collectively called the passive regulation system. In addition to passive regulation, the human body is capable of active regulation. The Fiala Thermoregulation model considers two means of active regulation: sweating for warm/hot environments and shivering for cool/cold environments.

In Simcenter STAR-CCM+, the bioheat equation is discretized on a thermal network. The bioheat equation for a thermal network

i

, which is connected to one or more network nodes

j

, is given by:

Figure 2. EQUATION_DISPLAY

\frac{d}{d T} (C_{p, i} T_{i}) + \underset{}{\sum_{j} \frac{T_{i} - T_{j}}{R_{i j}} + β V_{i} (T_{i} - T_{bla}) = q_{m} V_{i}}

(1802)

where:

$C_{p, i}$ is thermal heat capacity of node $i$ .
$T_{i}$ is the temperature of node $i$ .
$T_{j}$ is the temperature of node $j$ .
$R_{i j}$ is absolute thermal resistance between nodes $i$ and $j$ .
$β$ is the time-dependent calorimetric equivalent of the blood flow rate through the node.
$V_{i}$ is the volume of node $i$ .