Home
Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
Multiphase Flow
The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating multiphase fluid flow problems
Lagrangian: Solid Particle Erosion
This tutorial demonstrates how to set up an erosion modeling analysis in Simcenter STAR-CCM+. It simulates the erosion that is caused by solid particles in a liquid flow.
Defining Field Functions for the Restitution Coefficients
Create field functions to represent the restitution coefficients.

Share

Link: copied

Breadcrumb: copied

Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
- Using Tutorial Macros and Files
  Macros, input files, and final simulation files for a range of tutorials are provided as an optional download package on the Support Center website. These macros and final simulation files are provided as an aid to the written tutorials, so that you can check your final results against the downloaded files, or against a simulation that is built and run using the macros.
- Introduction
  Welcome to the Simcenter STAR-CCM+ introductory tutorial. In this tutorial, you explore the important concepts and workflow. Complete this tutorial before attempting any others.
- Foundation Tutorials
  The foundation tutorials showcase the major features of Simcenter STAR-CCM+ in a series of short tutorials.
- Geometry
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for creating and working with parts and 3D-CAD.
- Mesh
  The tutorials in this set illustrate various STAR-CCM+ features for building CFD meshes.
- Incompressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for incompressible fluid flows as well as porosity and solution recording
- Compressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for compressible fluid flows as well as harmonic balance.
- Heat Transfer and Radiation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for heat transfer, radiation, and thermal comfort.
- Multiphase Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating multiphase fluid flow problems
  - VOF: Gravity-Driven Flow
    This tutorial demonstrates how to set up a gravity-driven flow problem in Simcenter STAR-CCM+. It simulates two-dimensional gravity-driven compressible flow through a channel connecting two chambers.
  - VOF: Capillary Effects
    This tutorial demonstrates how to set up a capillary effects problem in Simcenter STAR-CCM+. It simulates two-dimensional forced flow of liquid glycerine through a nozzle and into an air-filled chamber at atmospheric pressure.
  - VOF: Cavitation
    This tutorial demonstrates how to set up a cavitation problem in Simcenter STAR-CCM+. It simulates a two-dimensional forced flow of water through a nozzle and into an air-filled chamber at atmospheric pressure.
  - VOF: Boiling
    This tutorial demonstrates how to set up a boiling problem in Simcenter STAR-CCM+. It simulates water boiling as it flows over a heated surface.
  - VOF: Melting-Solidification
    This tutorial demonstrates how to set up a melting and solidification analysis in Simcenter STAR-CCM+. It simulates the freezing of water in a pipe.
  - VOF: Tank Sloshing with Adaptive Meshing
    To reduce the computational time and resources required for VOF multiphase simulations, Simcenter STAR-CCM+ provides both Adaptive Mesh Refinement (AMR) and Adaptive Time-Stepping. AMR provides adaptation in space and Adaptive Time-Stepping provides adaptation in time. Together, these models improve the resolution of the interface with minimum computational effort by adjusting the mesh and the time-step during the simulation. Additionally, Simcenter STAR-CCM+ offers the Implicit Multi-stepping VOF solver which can be used to decrease computational costs further by sub-stepping the volume fraction transport equation to obtain a sharp interface while allowing for a larger flow time-step.
  - Lagrangian: Particle-Laden Flow
    This tutorial demonstrates how to set up a simple Lagrangian multiphase analysis in Simcenter STAR-CCM+. It simulates a particle-laden flow of air through a partially blocked elbow duct.
  - Lagrangian: Solid Particle Erosion
    This tutorial demonstrates how to set up an erosion modeling analysis in Simcenter STAR-CCM+. It simulates the erosion that is caused by solid particles in a liquid flow.
    - Prerequisites
      The instructions in the Lagrangian: Solid Particle Erosion tutorial assume that you are already familiar with certain techniques in Simcenter STAR-CCM+.
    - Importing the Mesh and Naming the Simulation
      Launch Simcenter STAR-CCM+, import the supplied geometry, and save the simulation.
    - Visualizing the Imported Geometry
      Examine the Geometry Scene 1 display in the Graphics window.
    - Selecting the Physics Models
      Physics models define the primary variables of the simulation, including pressure, temperature, velocity, and what mathematical formulation is used to generate the solution.
    - Selecting the Lagrangian Phase Models
      Create the Lagrangian phase and select the appropriate phase models.
    - Setting the Material Properties
      Define the material properties of the continuous and Lagrangian phases.
    - Setting the Lagrangian Phase Model Properties
      Define the Lagrangian phase model properties. The Drag Force model uses the default method for the Drag Coefficient, which is the Schiller-Naumann correlation.
    - Defining Field Functions for the Restitution Coefficients
      Create field functions to represent the restitution coefficients.
    - Setting the Lagrangian Phase Boundary Conditions
      Define the Lagrangian phase boundary conditions.
    - Setting the Erosion Model
      Select the appropriate erosion model.
    - Setting Continuous Phase Boundary Conditions
      Define the continuous phase boundary conditions.
    - Setting Up the Injector
      Define the injector that is used to introduce the particles into the solution domain.
    - Setting Solver Parameters and Stopping Criteria
      Set the appropriate solver parameters and stopping criteria for the simulation.
    - Visualizing the Solution
      Create a scalar scene to view the results of the simulation.
    - Reporting and Plotting the Pressure Drop
      Create reports of average pressure at the inlet and outlet boundaries, and use the reports in a field function that gives the pressure drop.
    - Initializing and Running the Simulation
      Preparation of the simulation is now complete, and the simulation can be run.
    - Visualizing the Results
      Create a scalar scene to view the results of the simulation.
    - Estimating the Overall Erosion Rate
      Create a field function and report to estimate the overall erosion rate.
    - Comparison with Experimental Data
      The simulation results are compared with experimental data.
    - Implementing Alternative Functions for Erosion Ratio
      Erosion equations are often tuned for a particular material/sand combination that are based on experimental testing. In this section, implement the model that was developed by Zhang et al. at the Erosion/Corrosion Research Center in Tulsa as an example.
    - Summary
      This tutorial demonstrated how to set up an erosion modeling analysis in Simcenter STAR-CCM+.
    - Bibliography
      This tutorial references the following papers.
  - Eulerian: Hibiki’s Bubble Column
    This tutorial demonstrates how to model a Eulerian multiphase turbulent flow in Simcenter STAR-CCM+.
  - Eulerian: Mixture Settling
    Settling tanks/separators are widely used in the industry for the purpose of separating a fluid mixture into its gaseous and liquid phases. Separator designs include horizontal and vertical configurations that account for different stages of the process, ranging from absorbing the momentum of incoming fluid to achieving the desired phase separation.
  - Eulerian: Bubble Formation in a Fluidized Bed
    This tutorial demonstrates how to model bubble formation in a fluidized bed in Simcenter STAR-CCM+. It simulates the injection of gas into a fluidized bed and monitors the formation and growth of the bubble.
  - Eulerian: Aeration Tank Degassing
    In industry, aeration tanks facilitate the exchange of gases in various processes within a liquid medium. Degassing is a procedure that actively removes gases from a liquid, such as eliminating excess gases that can build up during the biological treatment of organic pollutants, a process particularly common in waste-water treatment.
  - Eulerian: Wall Boiling
    This tutorial validates the wall boiling model in Simcenter STAR-CCM+ against experimental void and temperature data for high-pressure forced convective boiling.
  - Eulerian: Conjugate Heat Transfer Wall Boiling
    This tutorial demonstrates how to set up a conjugate heat transfer wall boiling analysis in Simcenter STAR-CCM+. It simulates a nuclear fuel pin that is cooled using subcooled boiling under flow conditions typical in the first meter of a 3.7-m long BWR6 reactor channel.
  - Eulerian Multiple Flow Regimes: Pressurized Water Reactor
    This tutorial demonstrates how to use the Multiple Flow Regimes model in Simcenter STAR-CCM+ to simulate the counter-current air-water flow in a pressurized water reactor.
  - Eulerian: Pipe Flow with Multi-Speed AMUSIG
    The Adaptive Multiple Size-Group (AMUSIG) model predicts the size distribution of particles (droplets or bubbles) in a dispersed multiphase flow regime. This tutorial demonstrates how to use the AMUSIG model for predicting the size distribution of hexane droplets in water. The water is flowing up a vertical pipe in which a concentric orifice increases turbulence and so accelerates droplet breakup.
  - Eulerian: Suspension Rheology
    This tutorial demonstrates how to set up a Simcenter STAR-CCM+ simulation that models the flow of a non-Newtonian concentrated suspension.
  - Fluid Film: Liquid Film Flow
    This tutorial demonstrates how to use the fluid film modeling capability of Simcenter STAR-CCM+. It simulates the progress of a rectangular film of water flowing down the wall of a three-dimensional duct.
  - Fluid Film: Binary Liquid Film Flow with Evaporation and Edge Stripping
    This tutorial demonstrates how to use the fluid film modeling capability of Simcenter STAR-CCM+ to set up a multi-component film scenario with evaporation and edge stripping. It simulates the progress of a film mixture of water and ethylene glycol flowing down a partially heated wall.
  - Fluid Film - VOF: Rivulets on an Inclined Plane
    Situations occur where a thin film of liquid forms on a solid surface, for example, rainwater on the windshield of a car. This film can flow and accumulate, and gradually grow into a "thick" film, or a pool of liquid that can no longer be described as a fluid film. These situations are multi-scale problems which, if resolved on all scales (using the VOF multiphase model), would require significant computer resources.
  - Dispersed Multiphase: Airfoil Icing
    When aircraft pass through air containing supercooled liquid water droplets, it is possible for the droplets to impact the aircraft surface and form layers of ice. Ice formation on an aircraft wing changes the aerodynamic properties of the wing, and leads to loss of lift, increase in drag, and a change in pressure distribution. Simcenter STAR-CCM+ provides a technique for simulating the formation of ice on airfoils. This technique relies on the Dispersed Multiphase model to represent the liquid droplets in the air surrounding the airfoil.
  - Hybrid Multiphase: Fountain
    In Simcenter STAR-CCM+ modeling, the term hybrid multiphase refers to modeling multiple flow regimes of a phase material using a combination of several different multiphase models. This modeling capability widens the range of real life multiphase flows that you can simulate.
  - Mixture Multiphase with Large Scale Interfaces: Gear Lubrication
    The Mixture Multiphase (MMP) model is suitable for modeling dispersed multiphase mixtures, where the mixture of phases is represented by weighted physical properties. A single set of conservation equations for mass, momentum, and energy is solved for the mixture together with transport equations for phase volume fractions.
  - Viscous Multiphase: Two-Layer Pipe Co-Extrusion
  - Smoothed-Particle Hydrodynamics (SPH): Gearbox Lubrication
    Gear mechanisms require adequate lubrication for long-term optimum performance and efficiency. Simcenter STAR-CCM+ provides the Smoothed-Particle Hydrodynamics (SPH) model with which you can simulate the flow of lubricant around the parts of a gear mechanism and determine whether adjustments are necessary.
- Discrete Element Method
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating Discrete Element Method problems
- Motion
  The tutorials in this set illustrate various STAR-CCM+ features for simulating problems with moving geometries and meshes, dynamic fluid body interaction, and rigid body motion:
- Reacting Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating reacting flows such as combustion.
- Solid Stress
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for computing deformation, strain, and stresses in solid regions. They also show how such computations can be coupled to the fluid behavior in an analysis of fluid-structure interaction.
- Aeroacoustics
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for solving aeroacoustic simulations.
- Electromagnetism
  The following tutorials illustrate features for solving problems that involve electromagnetic fields.
- Electrochemistry
  The following tutorial demonstrates chemical reactions induced by an electrical current.
- Battery
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for setting up a battery model:
- Automation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ automation and macro features.
- Design Exploration
  The tutorials in this set illustrate various features for running design exploration studies in Design Manager.
- Coupling with CAE Codes
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for coupling with CAE codes:
- Analysis Methods
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for analysing and visualizing simulation data.
- Simcenter STAR-CCM+ In-cylinder
  The tutorials in this set illustrate features for simulating internal combustion engines in Simcenter STAR-CCM+ using the dedicated add-on Simcenter STAR-CCM+ In-cylinder.

Defining Field Functions for the Restitution Coefficients

Create field functions to represent the restitution coefficients.

Restitution coefficients are used to predict the angle with which a particle rebounds off a solid wall. In this tutorial, the relations that were developed by Forder et al. ([967]) are used:

$ϵ_{T} = 1 - 0.78 α_{p} + 0.84 α_{p}^{2} - 0.21 α_{p}^{3} + 0.028 α_{p}^{4} - 0.022 α_{p}^{5}$

$ϵ_{N} = 0.988 - 0.78 α_{p} + 0.19 α_{p}^{2} - 0.024 α_{p}^{3} + 0.027 α_{p}^{4}$

Represent these equations in Simcenter STAR-CCM+ using user field functions. The quantities referred to in user field functions must come from the predefined system field functions or other user field functions. In this simulation you require a predefined system field function for the particle incidence angle.

To define field functions for the restitution coefficients:

Open the Automation > Field Functions node.
Scroll down the list until the Particle Incidence Angle function is visible.
Select Particle Incidence Angle and note the value of the Function Name property.

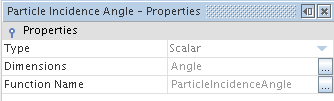
Having noted the required name of ParticleIncidenceAngle, it is now possible to create the function for the Normal Restitution Coefficient.

Right-click the Automation > Field Functions node and select New > Scalar from the pop-up menu.

A new User Field Function 1 node appears in the object tree.
Rename User Field Function 1 to ENormal.

Select ENormal and set the following properties:


Property	Setting
Function Name	NormalRestitutionCoefficient
Dimensions	Dimensionless
Definition	0.988 - 0.78$ParticleIncidenceAngle + 0.19(pow($ParticleIncidenceAngle, 2)) - 0.024(pow($ParticleIncidenceAngle, 3)) + 0.027(pow($ParticleIncidenceAngle, 4))

The same steps are now repeated for the tangential restitution coefficient.

Right-click the Automation > Field Functions node and select New > Scalar from the pop-up menu.

A new User Field Function 1 node appears in the object tree.
Rename User Field Function 1 to ETan.

Select ETan and set the following properties:


Property	Setting
Function Name	TangentialRestitutionCoefficient
Dimensions	Dimensionless
Definition	1 - 0.78$ParticleIncidenceAngle + 0.84(pow($ParticleIncidenceAngle, 2)) - 0.21(pow($ParticleIncidenceAngle, 3)) + 0.028(pow($ParticleIncidenceAngle, 4)) - 0.022*(pow($ParticleIncidenceAngle, 5))