Home
Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
Incompressible Flow
The tutorials in this set illustrate various Simcenter STAR-CCM+ features for incompressible fluid flows as well as porosity and solution recording
Porous Resistance: Isotropic Media
This tutorial models flow through a catalyst geometry.

Link: copied

Breadcrumb: copied

Tutorials
Tutorials show you how to use Simcenter STAR-CCM+ for various applications in a step-by-step format with recommendations for setup, initialization and steps of the solution process specific to the application. Macro and simulation files are available for download for a large proportion of cases.
- Using Tutorial Macros and Files
  Macros, input files, and final simulation files for a range of tutorials are provided as an optional download package on the Support Center website. These macros and final simulation files are provided as an aid to the written tutorials, so that you can check your final results against the downloaded files, or against a simulation that is built and run using the macros.
- Introduction
  Welcome to the Simcenter STAR-CCM+ introductory tutorial. In this tutorial, you explore the important concepts and workflow. Complete this tutorial before attempting any others.
- Foundation Tutorials
  The foundation tutorials showcase the major features of Simcenter STAR-CCM+ in a series of short tutorials.
- Geometry
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for creating and working with parts and 3D-CAD.
- Mesh
  The tutorials in this set illustrate various STAR-CCM+ features for building CFD meshes.
- Incompressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for incompressible fluid flows as well as porosity and solution recording
  - Steady Flow: Lid-Driven Cavity Flow
    This tutorial demonstrates the performance of Simcenter STAR-CCM+ in solving a traditional square lid-driven cavity flow. The problem geometry consists of a two-dimensional 1 m² cavity. The cavity is covered by an impermeable wall that moves in the x-direction with constant velocity of 1 m/s. A stretched quadrilateral mesh with 6400 cells is used.
  - Steady Flow: Channel Flow with Multiple Meshes
    This tutorial describes a steady airflow simulation over an obstacle that is mounted at the bottom wall of a three-dimensional channel.
  - Steady Flow: Laminar and Turbulent Flow in an S-Bend
    This tutorial demonstrates the flow of an incompressible gas through an s-bend of constant diameter (2 cm), for both laminar and turbulent flow. The first part of the tutorial covers the laminar flow, with a Reynolds number (Re) of 500, and the second part covers the turbulent flow, Re = 50,000. The same pipe geometry is used in both cases.
  - Steady Flow: Backward Facing Step
    Steady flow over a backward facing step is a typical scenario to investigate the behaviour of reattaching flows. Understanding the behaviour of the flow is crucial for many applications such as designing heat exhangers, evalutating aerodynamic performance and improving flow control strategies.
  - Anisotropic Flow: Cyclone Separator
    The flow inside a cyclone separator is characterised by strong swirling motion and three-dimensional boundary layers. Properly accounting for these effects is a challenging problem for CFD simulations. This tutorial presents the initial step in setting up a coarse mesh cyclone flow simulation.
  - Porous Resistance: Isotropic Media
    This tutorial models flow through a catalyst geometry.
    - Prerequisites
      The instructions in the Porous Resistance: Isotropic Media tutorial assume that you are already familiar with certain techniques in Simcenter STAR-CCM+.
    - Importing the Mesh and Naming the Simulation
      Import a polyhedral mesh from the incompressibleFlow folder, and save and name the new simulation.
    - Visualizing the Imported Mesh
      A geometry scene was automatically created after the import process. Examine the Geometry Scene 1 display in the Graphics window. Initially all parts of the mesh are shown as solid, colored surfaces.
    - Scaling the Mesh
      The original mesh was not built to scale and therefore requires scaling so that the dimensions of the porous region are 0.1 x 0.03 x 0.1 meters.
    - Setting Up the Models
      Models define the primary variables of the simulation, including pressure, temperature and velocity, and what mathematical formulation is used to generate the solution. In this example, the flow is turbulent and incompressible. Use the Segregated Flow model together with the standard K-Epsilon turbulence model.
    - Setting Boundary Conditions and Values
      The default boundary conditions on the wall and outlet boundaries are suitable for this analysis so the only user specifications required are on the inlet boundary. A fixed velocity of 20 m/s and appropriate turbulence parameters need to be specified there.
    - Specifying Porosity Coefficients
      As discussed in the introduction to this tutorial, the porous region is defined by its inertial and viscous resistance coefficients, which are 25 kg/m⁴ and 1500 kg/m³s, respectively. As the porous region is isotropic, these values hold in all directions. The coefficients, along with the turbulence parameters in the porous region, must now be specified.
    - Monitoring the Run Progress
      As part of the post-processing operations, make sure that the calculated pressure drop across the porous region is close to the theoretical drop given by [eqnlink.
    - Setting Stopping Criteria
      Rather than arranging for the analysis to run for a set number of iterations, it is often useful to specify stopping criteria based on residual values and monitored quantities. For this simulation, define a stopping criterion that checks whether the porous region pressure drop monitor has reached a steady value.
    - Visualizing the Solution
      View the velocity vector field as the solution develops on a plane bisecting the fluid and porous regions.
    - Running the Simulation
      Run the simulation and observe the Residuals plot, the monitor plots, and the vector scene.
    - Visualizing Results
      Examine the vector scene in detail.
    - Validating the Results
      As discussed at the start of the tutorial, the calculated pressure drop across the porous region can be compared to the theoretical pressure drop derived from the mass flow rate.
    - Summary
      This tutorial models flow through the catalyst geometry.
  - Porous Resistance: Orthotropic Media
    This tutorial solves the same problem as the Porous Resistance: Isotropic Media, except that the fluid in the porous region cannot flow in any direction other than the bulk flow (y-) direction.
  - Solution Recording and Playback: Vortex Shedding
    This tutorial demonstrates how to use the solution recording and playback module for capturing the results of transient phenomena.
  - Generalized Newtonian Fluid: Flow in a Static Mixer
    This tutorial demonstrates the process of setting up and analyzing the flow of a viscous fluid through a static mixer.
  - Viscoelastic Flow: Basic Extrusion
    This tutorial illustrates the extrusion of molten rubber through a die.
  - Material Calibration: Curve Fitting Non-Newtonian Model Parameters
    This tutorial illustrates the workflow for calibrating rheological model parameters from experimental rheological data through curve-fitting.
  - Polymer Melt Extrusion: Film Casting
    In industry, film casting is a common process for producing thin polymeric films. Cast films are used for applications such as food and textile packaging, stretch wraps, or plastic bags. Simcenter STAR-CCM+ provides a combination of the Film Casting model and the Free Surface model that allows you to simulate that process and to investigate the impact of various parameters on the resulting film.
- Compressible Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for compressible fluid flows as well as harmonic balance.
- Heat Transfer and Radiation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for heat transfer, radiation, and thermal comfort.
- Multiphase Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating multiphase fluid flow problems
- Discrete Element Method
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating Discrete Element Method problems
- Motion
  The tutorials in this set illustrate various STAR-CCM+ features for simulating problems with moving geometries and meshes, dynamic fluid body interaction, and rigid body motion:
- Reacting Flow
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for simulating reacting flows such as combustion.
- Solid Stress
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for computing deformation, strain, and stresses in solid regions. They also show how such computations can be coupled to the fluid behavior in an analysis of fluid-structure interaction.
- Aeroacoustics
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for solving aeroacoustic simulations.
- Electromagnetism
  The following tutorials illustrate features for solving problems that involve electromagnetic fields.
- Electrochemistry
  The following tutorial demonstrates chemical reactions induced by an electrical current.
- Battery
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for setting up a battery model:
- Automation
  The tutorials in this set illustrate various Simcenter STAR-CCM+ automation and macro features.
- Design Exploration
  The tutorials in this set illustrate various features for running design exploration studies in Design Manager.
- Coupling with CAE Codes
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for coupling with CAE codes:
- Analysis Methods
  The tutorials in this set illustrate various Simcenter STAR-CCM+ features for analysing and visualizing simulation data.
- Simcenter STAR-CCM+ In-cylinder
  The tutorials in this set illustrate features for simulating internal combustion engines in Simcenter STAR-CCM+ using the dedicated add-on Simcenter STAR-CCM+ In-cylinder.

Porous Resistance: Isotropic Media

This tutorial models flow through a catalyst geometry.

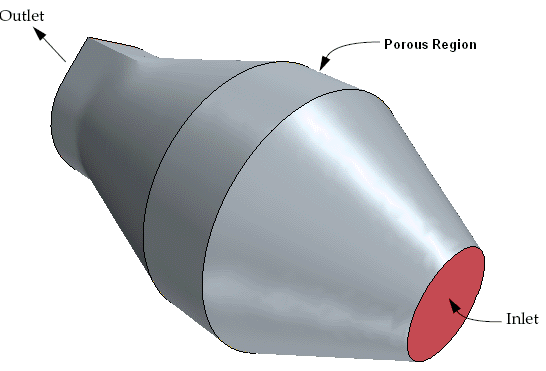
The geometry is shown below. The catalyst material at the center of this geometry is modeled as a cylindrical porous region of length 0.03 m and diameter 0.1 m.

In the porous region, the theoretical pressure drop per unit length can be determined using the equation:

\frac{Δ p}{L} = - (P_{i} | v | + P_{v}) v

Where $v$ is the superficial velocity through the medium and $P_{i}, P_{v}$ are coefficients defining the porous resistance, known as the inertial resistance and viscous resistance, respectively.

Values for the resistance coefficients can be measured experimentally or derived using various empirical relationships, depending on the exact nature of the problem. In this case, $P_{i}$ = 25 kg/m⁴ and $P_{v}$ = 1500 kg/m³s. These values are roughly what you would expect from an isotropic porous catalyst.