Computing Adjoint Error Estimates
Adjoint Error Estimates highlight locations in the flow where high numerical inaccuracy impacts the accuracy of the respective cost function. You compute Adjoint Error Estimates for specific cost functions, (such as pressure drop in a channel or airfoil drag), after the Adjoint solution is complete. You access Adjoint Error Estimates through field functions.
- A converged second-order flow solution
- Appropriate cost functions
- A converged second-order Adjoint solution with respect to the desired cost function
- Recomputes the convective flux of the Navier-Stokes equations by using the MUSCL third-order/CD discretization scheme.
- Subtracts the second-order computed cell-residual from the third-order MUSCL cell-residual.
This difference is a simple estimate of the true numerical error that is present in the second-order solution. The true numerical error of the solution is theoretically calculated by using a higher-order discretization scheme and a fine mesh.
- To obtain the Adjoint Error Estimate for each cell, the field of differences in cell-residual from the previous step is multiplied with the Adjoint solution for a given cost function.
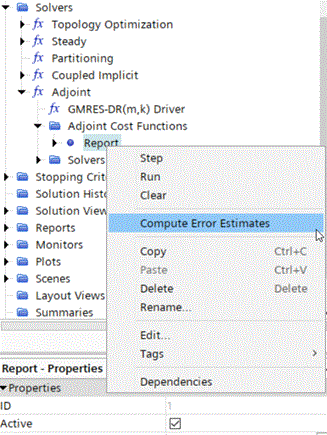
To compute Adjoint Error Estimates for all defined cost functions:
-
Right-click the node and select Compute Error Estimates.
For each defined cost function, an field function becomes available.Here, you see a contour plot of the Adjoint Error Estimate of the cost function Force (here defined as force component in the Z direction corresponding to drag). This cost function is applied to the simulation of aerodynamics around a car.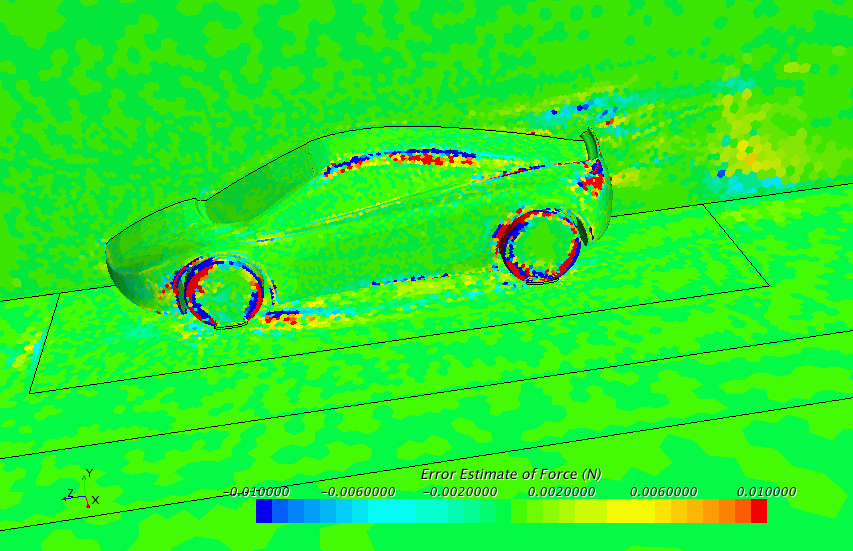
In locations where the error estimate deviates from zero by a certain threshold, the mesh can be refined to improve the drag.
-
Create a
Sum Report and set
Scalar Field Function to
Error Estimate of [Cost Function].
This sum report gives an estimate of the cost function variation as a result of changing the flow convection order of accuracy from second order to MUSCL.