Home
Pre-Processing
Simcenter STAR-CCM+ solves physics problems on a computational mesh. To provide this mesh, you first define geometry using internal or external tools, and then create a mesh pipeline whose operations generate the mesh in repeatable steps.
Meshing
A mesh is a discretized representation of a geometric domain. This domain can include real-world geometry, its content, and its surrounding environment.
Volume Meshers
Simcenter STAR-CCM+ contains different types of meshers that can be used to generate a volume mesh starting from a suitably prepared surface mesh.
Tetrahedral Mesher
Tetrahedral meshes provide an efficient and simple solution for complex mesh generation problems.

Share

Link: copied

Breadcrumb: copied

Pre-Processing
Simcenter STAR-CCM+ solves physics problems on a computational mesh. To provide this mesh, you first define geometry using internal or external tools, and then create a mesh pipeline whose operations generate the mesh in repeatable steps.
- 3D-CAD
  3D-CAD is a feature-based parametric modeler within Simcenter STAR-CCM+ that allows you to build geometries from scratch. The geometries that you create with 3D-CAD are stored as 3D-CAD models, which you can then convert to geometry parts for integration with the meshing and simulation process.
- Modeling Geometry
  This part of the User Guide describes how to use 3D-CAD, the parametric solid modeler available within Simcenter STAR-CCM+. It also describes the features and tools available for further preparation of the geometry model and its surfaces.
- The Surface Repair Tool
  The Surface Repair tool diagnoses errors in, and provides repair tools for, tessellated surfaces and part curves. The same tool allows you to reorganize discretized geometry by searching for face-based features and attributes then assigning the results to new or existing part surfaces or curves.
- Defining the Regions Layout
  An essential part of the process in setting up your simulation is to define the relationship between geometry parts and regions, boundaries, and interfaces.
- Meshing
  A mesh is a discretized representation of a geometric domain. This domain can include real-world geometry, its content, and its surrounding environment.
  - Mesh Construction
    Within a bounding volume defined by geometrical surfaces, Simcenter STAR-CCM+ can construct meshes for finite volume and finite element solvers.
  - Meshers in Simcenter STAR-CCM+
    The meshers in Simcenter STAR-CCM+ generate surface and volume meshes for geometry parts that are assigned to regions and make them ready for analysis.
  - Parts-Based Meshing
    Parts-based meshing (PBM) is a meshing strategy in which you create one or more mesh operations that define workflows for preparing, fixing, and processing geometry. A major benefit of PBM is that every mesh operation you create forms part of a linear and repeatable process.
  - The Meshing Workflow
    This section contains the recommended workflow for setting up and generating the volume mesh at the parts level.
  - Mesh Operations
    Mesh operations perform actions on geometry parts that you can easily repeat whenever their input parts or properties are changed.
  - Mesh Descriptions
    A mesh description is a version of a surface or volume mesh belonging to a geometry part. Geometry parts can have more than one surface mesh description associated with them. You create and change descriptions by importing surfaces or executing operations.
  - Custom Mesh Controls
    Custom controls override any default controls for the surface and volume meshers. This facility allows you to refine or coarsen the mesh for part curves, part surfaces, geometry parts, and specified volumes.
  - Surface Meshers
    Simcenter STAR-CCM+ contains meshing tools which can be used to help prepare a high-quality surface mesh before a volume mesh can be generated.
  - Volume Meshers
    Simcenter STAR-CCM+ contains different types of meshers that can be used to generate a volume mesh starting from a suitably prepared surface mesh.
    - Volume Meshers Overview
      This section introduces volume meshing.
    - Polyhedral Mesher
      Polyhedral meshes provide a balanced solution for complex mesh generation problems.
    - Tetrahedral Mesher
      Tetrahedral meshes provide an efficient and simple solution for complex mesh generation problems.
      - Conformal Tetrahedral Meshing Across Operations
        When using the tetrahedral mesher, you can generate a conformal mesh across parts that are assigned to different Automated Mesh Operations.
    - Trimmed Cell Mesher
      The trimmed cell mesher provides a robust and efficient method of producing a high-quality grid for both simple and complex mesh generation problems.
    - Prism Layer Mesher
      In an Automated Mesh operation, you can use the Prism Layer Mesher in combination with a core volume mesher to generate orthogonal prismatic cell layers at wall surfaces. This layer of cells is necessary to improve the accuracy of the flow solution at wall boundaries.
    - Advancing Layer Mesher
      The advancing layer mesher generates layers of prismatic cells around the surfaces of regions or parts and fills the remaining void with polyhedral cells. This mesher either uses the initial triangular or quadrilateral surface mesh, or converts the triangular mesh to a polygonal or quad surface mesh, depending on the Surface Element Type that you select. This surface mesh is then advanced into the region volume to form cell layers. Some advantages of this approach are a conformal match on either side of an interface, and the ability to generate thicker and more uniform cell layers.
    - Thin Mesher
      The Thin mesher is used to generate a prismatic type volume mesh for thin volumes within parts or regions. Thick or bulk portions of the same geometry are meshed with the core volume mesher.
    - Generalized Cylinder Mesher
      The generalized cylinder mesher generates a swept mesh along the length of parts that are cylindrical. This type of mesher uses the polyhedral and tetrahedral volume meshers to generate a conformal mesh.
    - Volume Mesher Controls and Values
      This section details the common controls, values, and right-click actions for all volume meshers. Controls that are specific to one mesher are detailed in the reference section for that mesher.
  - Mesh Refinement
    Simcenter STAR-CCM+ can refine the mesh by approximating the wake region or using solution-based approach. These features allow you to achieve efficient refinement by reducing the cell size in areas of interest.
  - Directed Meshing
    Directed meshing is a method for generating high quality swept meshes on geometries in Simcenter STAR-CCM+. The method operates by sweeping a mesh from the surfaces of a geometry through its volume onto a facing target surface.
  - Two Dimensional and Axisymmetric Meshes
    The use of a one-cell-thick three-dimensional mesh is much less efficient than using a real two-dimensional mesh for two-dimensional and axisymmetric simulations. When circumstances allow, use real two-dimensional meshes.
  - Turbomachinery Mesh
    Turbomachinery applications with axial blades typically require a flow-aligned, structured mesh. This type of mesh has implicit connectivity and a fixed number of vertex or face neighbors, leading to a more accurate solution.
  - Mesh Visualization
    You can visualize any mesh representation in Simcenter STAR-CCM+. After you have imported or generated a mesh, you visualize it to check the cell quality and mesh validity.
  - Checking the Surface Mesh
    The volume mesh quality is directly dependent on the surface mesh quality. Therefore, it is crucial to make sure that all surface meshes are of good quality.
  - Checking the Volume Mesh
    This section describes the tools available for checking the validity and quality of the volume mesh, and for diagnosing problem areas. Such problems can then be fixed, either inside Simcenter STAR-CCM+ or in the originating mesh generator.
  - Meshing Field Functions Reference
    This section contains a list of field functions that are related to meshing.
  - Working With Representations
    This section provides information on representations as a useful part of the meshing process.
  - Scaling the Entire Mesh
    Scaling the mesh is important as the units of the model must be in meters before running an analysis.
  - Working with Baffles
  - Exporting Mesh and Solution Data
    This section outlines the steps for exporting Simcenter STAR-CCM+ mesh and solution data to formats that can be used in other CAE packages.
  - Multi-Region Meshing
    This section outlines the surface requirements for performing multi-region meshing, as well as step-by-step instructions when starting from surface imports that result in single region and multiple regions definitions. Additionally, guidelines are provided on what the best approaches are for exporting surface data from CAD packages when multiple regions are required.

Tetrahedral Mesher

Tetrahedral meshes provide an efficient and simple solution for complex mesh generation problems.

Out of the three provided models, the tetrahedral is the fastest and uses the least amount of memory for a given number of cells. Multi-part or multi-region meshes with a conformal mesh interface are allowed.

The tetrahedral meshing model utilizes the tetrahedral cell shape in order to build the core mesh. In Simcenter STAR-CCM+, the Delaunay method is used to construct the mesh, which iteratively inserts points into the domain, forming high-quality tetrahedra in the process. The resulting mesh strictly conforms to the triangulation of the surface at the domain boundary, so the quality of the original surface mesh must be good to ensure a good quality volume mesh. When you generate a tetrahedral mesh from a quadrilateral surface mesh, pyramidal cells are created to transition from quadrilateral surface cells to triangular cells for the tetrahedral mesh. If you are using a quadrilateral surface mesh with the tetrahedral mesher and prism layer mesher, the surface mesh must contain isotropic quadrilateral elements only.

An example tetrahedral core mesh, using either a Triangular or Quad Dominant surface mesh, is shown below:

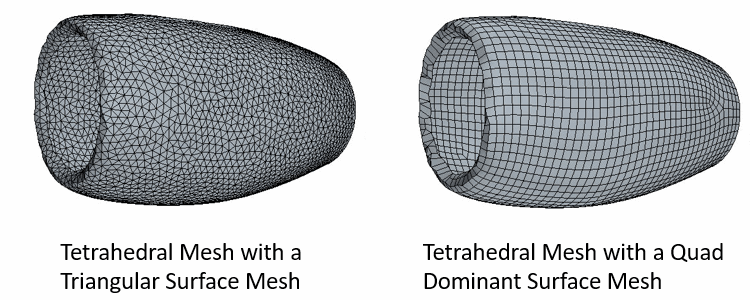
Cell sizes in the core mesh are governed by the Volume Growth Rate that determines how quickly cell sizes increase with increasing distance from the surface. Volumetric controls that are chosen from a range of prescribed shapes can also be included to set a specific cell size locally. The Volume Growth Rate also governs the rate at which cells grow from refinement zones to core mesh.

When the tetrahedral mesher is used with a periodic interface, it attempts to produce a conformal mesh for the boundary pair where possible.

Tetrahedral Mesher Expert Properties

The tetrahedral mesher expert properties that are common with the polyhedral mesher are documented in Volume Mesher Controls and Values.