Defining a Vortex Core Part
In Simcenter STAR-CCM+, the vortex core part automatically extracts vortex cores in a flow field.
Vortices are features in the flow data which are of great importance in fluid dynamics, both in theoretical and practical research. In some cases, vortices (turbulence) have to be impelled, for example to stimulate mixing of fluids, or to reduce drag. In other cases, vortices have to be prevented, for example around aircraft, where they can reduce lift.
The vortex core is the axis line around which the flow field rotates. The core provides a precise position of the vortex and also allows you to distinguish between different vortical structures close to each other.
Vortex core visualization belongs to the category of feature-based flow visualization techniques. The methods and algorithms in this category present the flow data in a higher level of abstraction. The flow data is described by a set of interesting and important objects or structures in the data called features. In fluid dynamics vortices, shock waves, separation lines, and attachment lines are examples of such features. Since only a small percentage of the data is of interest, and the features can be described compactly, it is possible to achieve considerable data reduction. This enables an interactive visualization of large amounts of fluid simulation data.
The vortex core extraction algorithm needs the velocity field and a three-dimensional region to generate poly lines representing vortex cores. It has three filtering parameters to filter out unwanted vortex cores.
There are many different definitions of vortices and likewise many different vortex detection algorithms. These definitions are based on certain field values being high or low, like high vorticity magnitude, high helicity magnitude, or low-pressure value. However, there is no accepted threshold value for what is considered high or low.
Definitions of features are usually implicit because they are procedural. However, precise mathematical definitions are attainable with the parallel vectors operator proposed by Peikert and Roth [137], [138]. This operator is an elementary operation on two vector fields, which in turn make it possible to define and calculate global line-type features of vector or scalar fields. The parallel vectors operator can be extended to unsteady fields. Advantages include:
- Comparing feature definitions
- Reusing algorithms and implementations
The parallel vectors operator causes the feature definition to work separately from the actual implementation. According to Roth and Peikert, along with various line-type features, the operator can implement algorithms to extract the following:
- Vortex core lines
- Lines of separation or attachment
Simcenter STAR-CCM+ uses the parallel vectors operator to implement the Eigenvector method for vortex core extraction proposed by Sujudi and Haimes [140], [136]. According to these authors, a rotational motion is present when the Jacobian (velocity gradient matrix) has a conjugate complex pair of Eigenvalues. The description of how the parallel vectors operator can be applied to the Eigenvector method is in the papers by Peikert and Roth [139], [137]as well as in the dissertation by Roth [138].
To create a vortex core:
- Follow the general procedure outlined in the section, Defining Derived Parts General Workflow. Choose the menu option,
- Specify the input parts and display option as described in the section, Defining Derived Parts General Workflow.
-
Complete the vortex core definition by specifying the following properties:
- Vector field
- Vortex strength
- Vortex quality
- Minimum core length
You can set all properties in either the in-place dialog or the Properties window.
For more information on the available properties, refer to the section Vortex Core Properties.You can display vortex cores on a geometry scene or as parts in streamline displayers. Within streamline displayers, you can display them as lines, ribbons, or tubes and color code them by a scalar as shown below.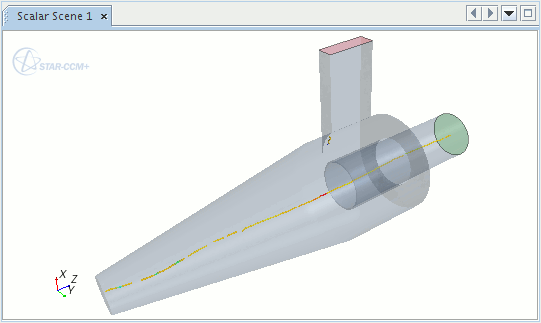
The vortex core can be used to seed streamlines in order to visualize the vortical structure as shown in the figure below.