Using the Chapman-Enskog Method for Dynamic Viscosity

This method becomes available for single- and multi-component gases once an energy model is included. This method is also activated when the Mathur-Saxena Averaging method is selected for dynamic viscosity.

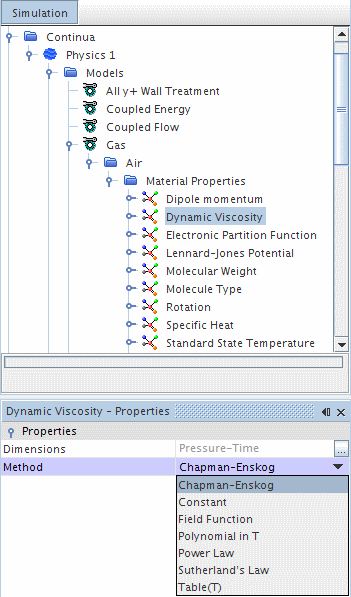
The dynamic viscosity of a simple gas, or of an individual component of a multi-component gas, is calculated with the Chapman-Enskog equation as follows:

where:

• $T\text{*}=kT/{\epsilon }_i$ is reduced temperature (dimensionless)
• $k$ is the Boltzmann constant
• ${\epsilon }_i$ is the potential energy of attraction of component $i$ ; values given in the standard material database, props.mdb, provided as a part of STAR-CCM+
• $\Omega \left(T\text{*}\right)$ is the collision integral
• ${\mu }_i$ is the viscosity of component $i$
• $M_i$ is the molecular weight of component $i$
• $T$ is temperature (in K)
• ${\sigma }_i$ is the collision diameter of component $i$ ; values given in the standard material database, props.mdb, provided as a part of STAR-CCM+

For a simple gas, there is only one value of $i$ .