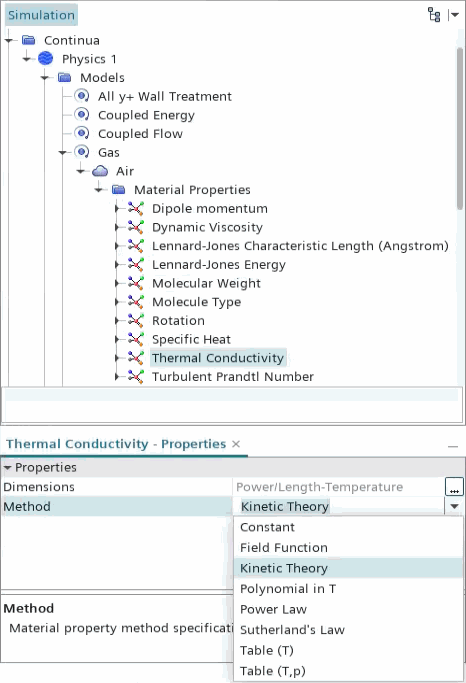
Using the Kinetic Theory Method for Thermal Conductivity

The Kinetic Theory method calculates the thermal conductivity of an individual gas component using kinetic theory.

The Kinetic Theory method for thermal conductivity is available for both single- and multi-component gases:

For single-component gases, the Kinetic Theory method is available under the Gas > [gas] > Material Properties > Thermal Conductivity node.
For multi-component gases, the Kinetic Theory method becomes available under the Multi-Component Gas > Gas Components > [gas] > Material Properties > Thermal Conductivity node for each gas component when you select the Mathur-Saxena Averaging method under the Multi-Component Gas > Material Properties > Thermal Conductivity node.

When this method is used, the following properties nodes appear for each gas species:

Dipole momentum — a measure of polarity of a covalent bond in the molecule (always given in Debye)
Lennard-Jones characteristic length — the collision diameter (always given in Angstroms)
Lennard-Jones energy — the potential energy of attraction (given in J/kmol)
Rotation — rotational relaxation collision number (non-dimensional)
Molecule Type — describes molecular structure; can be one of the following:
- 0: atom
- 1: linear molecule
- 2: nonlinear molecule

These properties have only one Method available for their calculation: Constant. Their values are used to calculate the thermal conductivity of the individual gas components using the Kinetic Theory method.

Calculation of Thermal Conductivity using the Kinetic Theory method

The thermal conductivity of a simple gas, or of an individual component of a multi-component gas, is calculated as follows:

Figure 1. EQUATION_DISPLAY

λ_{i} = \frac{μ_{i}}{M_{i}} (f_{t r a n s} C_{v, t r a n s} + f_{r o t} C_{v, r o t} + f_{v i b} C_{v, v i b})

(147)

where:

Figure 2. EQUATION_DISPLAY

f_{t r a n s} = \frac{5}{2} [1 - \frac{2}{π} \frac{C_{v, r o t}}{C_{v, t r a n s}} \frac{A}{B}]

(148)

Figure 3. EQUATION_DISPLAY

f_{r o t} = \frac{ρ D_{i i}}{μ_{i}} [1 + \frac{2}{π} \frac{A}{B}]

(149)

Figure 4. EQUATION_DISPLAY

f_{v i b} = \frac{ρ D_{i i}}{μ_{i}}

(150)

Figure 5. EQUATION_DISPLAY

A = \frac{5}{2} - \frac{ρ D_{i i}}{μ_{i}}

(151)

Figure 6. EQUATION_DISPLAY

B = z_{r o t} + \frac{2}{π} (\frac{5}{3} \frac{C_{v, r o t}}{R_{u}} + \frac{ρ D_{i i}}{μ_{i}})

(152)

Figure 7. EQUATION_DISPLAY

C_{v, t r a n s} = \frac{3}{2} R_{u}

(153)

Figure 8. EQUATION_DISPLAY

z_{r o t} = z_{r o t} (298) \frac{F (298)}{F (T)}

(154)

Figure 9. EQUATION_DISPLAY

F (T) = 1 + \frac{π^{3 / 2}}{2} {(\frac{ε / k}{T})}^{1 / 2} + (\frac{π^{2}}{4} + 2) \frac{ε / k}{T} + {π^{3 / 2} (\frac{ε / k}{T})}^{3 / 2}

(155)

and $z_{r o t} (298)$ is the value of the rotation collision number at 298 K, defined in the transport properties of the component.

For a linear molecule:

Figure 10. EQUATION_DISPLAY

C_{v, r o t} = R_{u}

(156)

Figure 11. EQUATION_DISPLAY

C_{v, v i b} = C_{v} - \frac{5}{2} R_{u}

(157)

$λ_{i}$ is the thermal conductivity of component $i$ .
$μ_{i}$ is the viscosity of component $i$ , $μ_{i} = μ_{i} (T)$ .
$M_{i}$ is the molecular weight of component $i$ .
$C_{v}$ is the molar specific heat at constant volume of the component.
$R_{u}$ is the universal gas constant.
$ε$ is the Lennard-Jones energy.
$k$ is the Boltzmann constant $= 1.3806503 \times 10^{- 23}$ m² kg s^-2 K^-1.

For a simple gas, there is only one value of $i$ .