Using Polynomial in T

This polynomial function is available for certain material properties.

The properties for this function are set in the Properties window.

Temperature polynomials are specified in piece-wise fashion where each interval $i$ spans the range ${Tr}_i$ to ${Tr}_{i+1}$ , has $m_i$ number of terms, and is of the form:

$X_{\left(T\right)}={\sum }_{k=0}^{m_i}{a_{i,k}\cdot T}^{bi,k}$ ; $Tr\le T\le {Tr}_{i+1}$

The polynomial has $n$ intervals with interval ranges:

${Tr}_0,{Tr}_1,{Tr}_2,\dots ,{Tr}_{n+1}$

The number of terms in each interval are:

$m_0,m_1,m_2,\dots ,m_n$

The exponents are:

$\begin{array}{c}{b}_{0,0},b_{0,1},b_{0,2},\dots ,b_{0,m_0}\\ b_{1,0},b_{1,1},b_{1,2},\dots ,b_{1,m_1}\\ \text{: : : :}\\ \text{: : : :}\\ b_{n,0},b_{n,1},b_{n,2},\dots ,b_{n,m_n}\end{array}$

The coefficients for the polynomial are:

$\begin{array}{c}{a}_{0,0},a_{0,1},a_{0,2},\dots ,a_{0,m_0}\\ a_{1,0},a_{1,1},a_{1,2},\dots ,a_{1,m_1}\\ \text{: : : :}\\ \text{: : : :}\\ a_{n,0},a_{n,1},a_{n,2},\dots ,a_{n,m_n}\end{array}$

Specify a temperature range of the polynomial sufficiently large such that the polynomial is not evaluated outside the range during the analysis. If the polynomial is ever evaluated outside the range, the property is assigned a value of the polynomial at the respective range limit.

Polynomial in T Properties

In the Properties window, a single property that is called Polynomial includes a property customizer (). Click that button to activate a customizer dialog with properties for working with polynomials in STAR-CCM+.

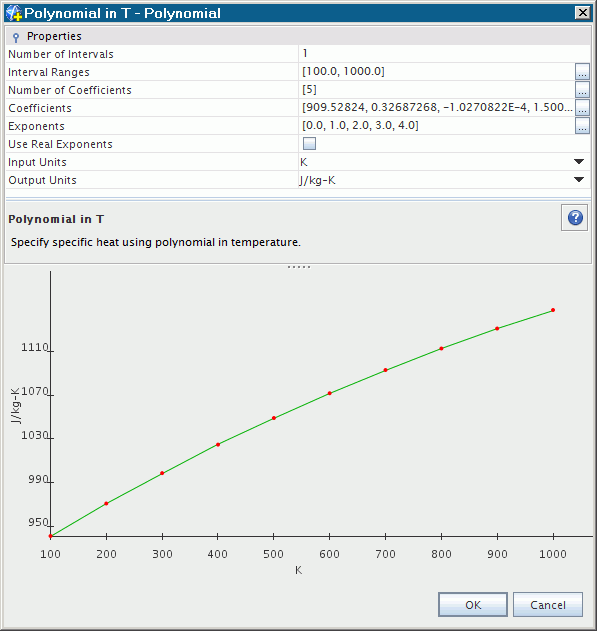
The plot in this dialog gets updated instantly with your changes. You can select units separately for each axis: Input Units for the x-axis, and Output Units for the y-axis. Unlike constant values, the polynomial coefficients and polynomial ranges (and the corresponding x- and y-axes on the polynomial plot) do not rescale when you change the units.

For the Coefficients property, commas separate the entries and the coefficients are in the following order:

$C_p\left(T\right)=C_{p0}+(C_{p1}\cdot T)+(C_{p2}\cdot T^2)+\dots +(C_{pn}\cdot T^n)$

A separate section describes an example of working with these properties.

Note

When using a polynomial in T with real exponents to specify the specific heat of a material, you are advised to define the polynomial on an absolute temperature scale by selecting either K and J/kg-K or R and Btu/lb-R as the values for Input Units and Output Units respectively. These selections avoid any difficulties that are associated with the integrations of $C_p\left(T\right)/T$ used to evaluate certain thermodynamic properties such as entropy and total pressure when $C_p\left(T\right)$ is specified on a non-absolute temperature scale that can pass through $T=0$ .